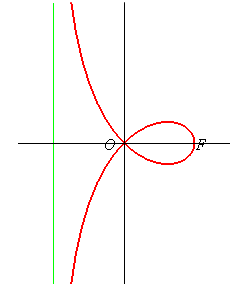Polar equation: (or turned by: ) Cartesian equation: . Rational circular cubic with double point. Cartesian parametrization:  (with ), or  (with ). Cartesian rational parametrization:    (with ), hence the complex parametrization: . If we consider the frame (F(0, a) (vertex of the loop), ), the polar equation simplifies to: , the complex equation can be written  with  and a complex parametrization is . Length of the loop: . Area of the loop: . Area between the curve and the asymptote: .

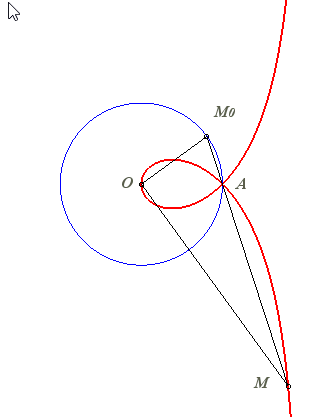
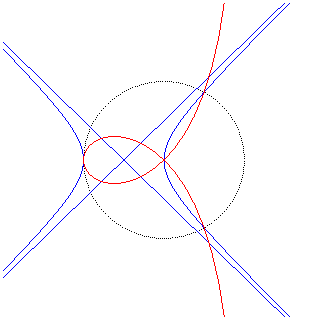
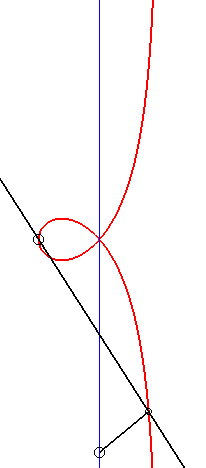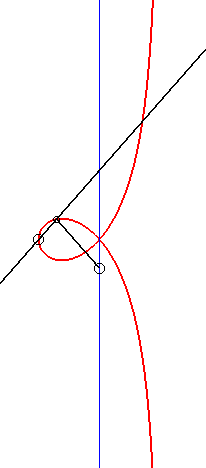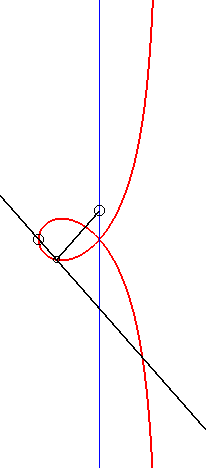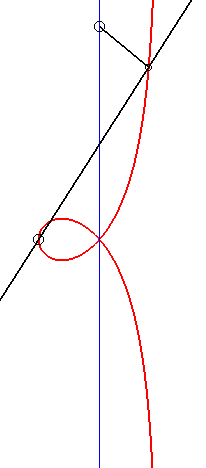
Given two points O and F, the right strophoid with vertex (or focus) F and centre O is the locus of the points M on a variable line (D) passing by F such that PM = PO where P is the intersection point between the line (D) and the line (D₀) perpendicular at O to (OF) (called axis of the strophoid); in other words, it is the strophoidal curve of (D₀ with respect to O and F (here, O is the origin of the frame and F is the point (a, 0)); it is a special case of the general strophoids. The point F is called focus because it is the singularity of this cubic.

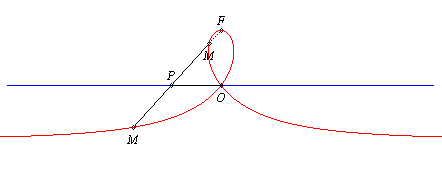PM = PO

Therefore, the right strophoid is also the locus of the contact points of the tangents passing by F to the circles (in blue opposite) that are tangent at O to the axis (D0), or also the locus of the intersection points between the circles, orthogonal to the previous ones (in green opposite), tangent at O to (OF), and the lines joining F to their centres.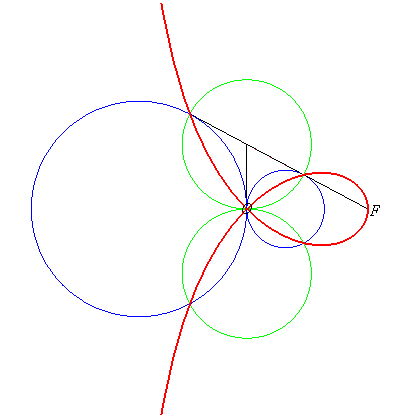

Here are two simple constructions:
 

A variable line (D') passing by O cuts the line (D1) parallel to (D0) passing by F at Q; the strophoid is the locus of the point M where the circle centred on F passing by Q cuts (D').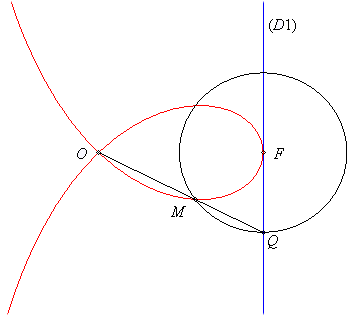
Given a point  on a circle with center O passing through A, the right strophoid is the locus of the point of intersection M of the line  with the perpendicular at O to  (construction by Pierre Apel). The transformation  is involutional by construction. Defined analytically by , it is a quadratic transformation.
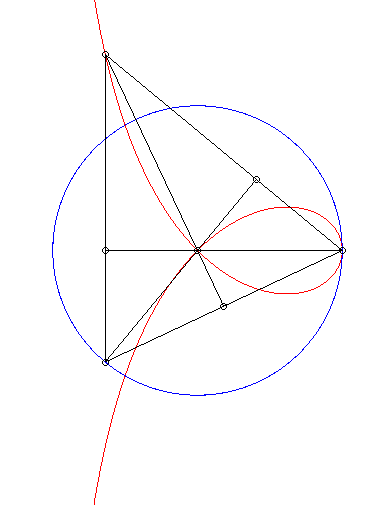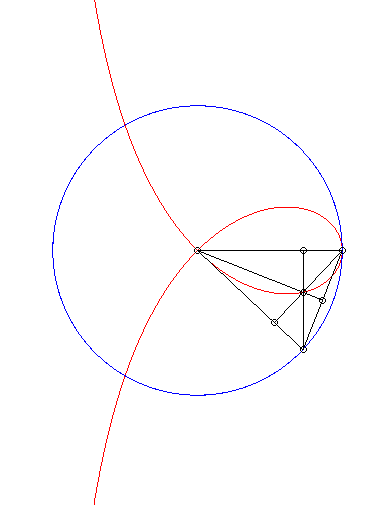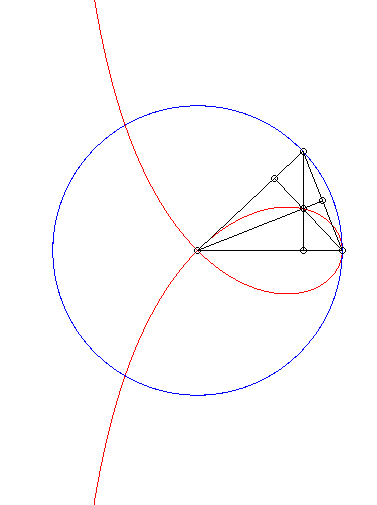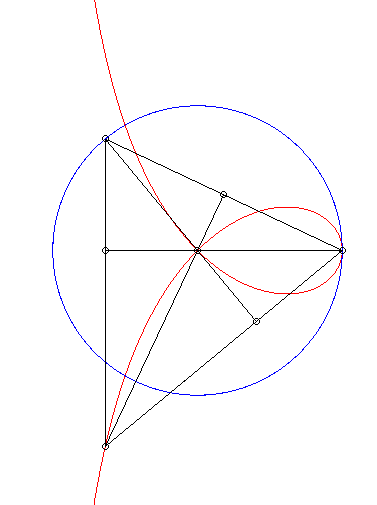
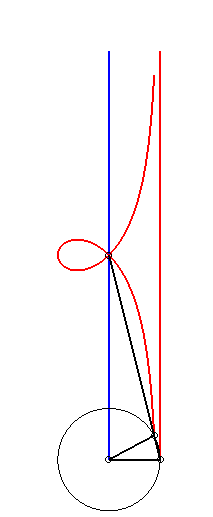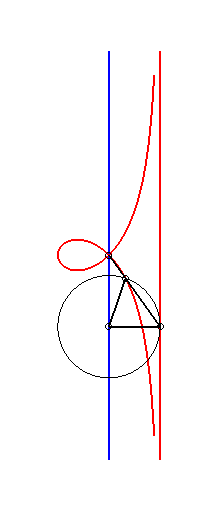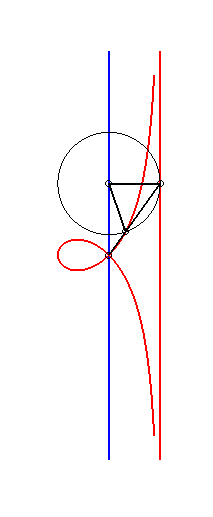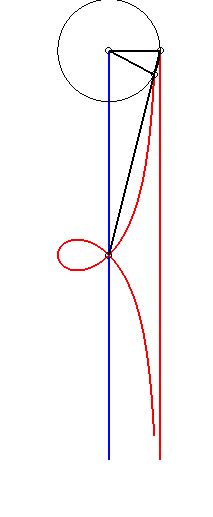
The right strophoid is the locus of the orthocentre of a triangle two vertices of which, A and B, are fixed while the third describes a circles with radius [AB]. Cf. a similar construction of the bicorn.
If (C) is the circle with centre O passing by F and G is the point diametrically opposed to F, then the right strophoid is the locus of the points M such that, if P is one of the intersection points between the perpendicular to (OF) passing by M and (C), then the line (OM) and (GP) are parallel (construction of Rosillo).

 
 

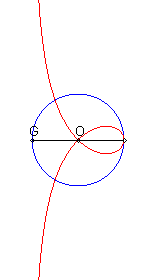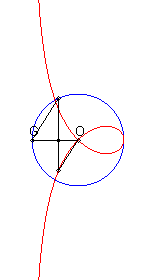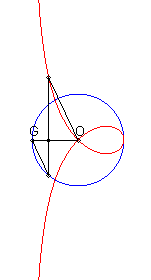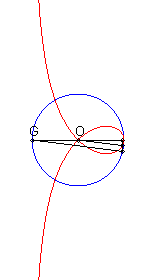The right strophoid also has the following elegant 3D construction: If (C) is the cylinder of revolution with axis (D0) and passing by F, then the right strophoid is the locus of the foci of the elliptic sections of the cylinder (C) by planes perpendicular to the plane of the strophoid and passing by F. This proves that the line (D0) is the median with pole F of the strophoid and itself.

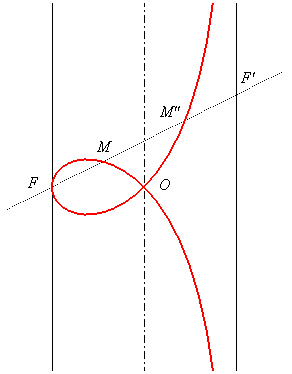
The foci of the ellipse with summits F and F' are M and M".

 
 

The polar equation  proves that the strophoid is the cissoid of the kappa and its asymptote.

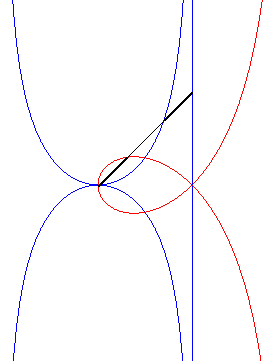The complex equation above proves that for a line passing by F, the two intersection points with the strophoid are inverses of one another by the inversion with reference circle the circle (C) with centre F passing by O:

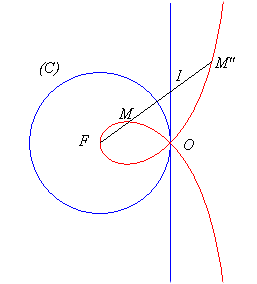
Like all rational circular cubics, the right strophoid can be defined as:

    - the cissoid with respect to O of a circle with radius a passing by O and a line parallel to the tangent at O and located at distance a from the circle (the asymptote of the strophoid); here the circle (C) passing by O with centre F:
 

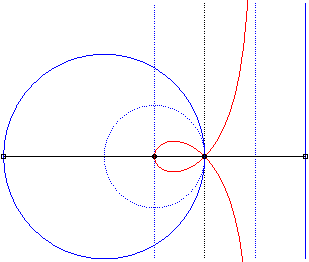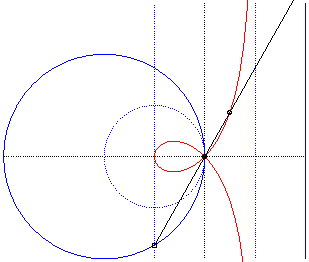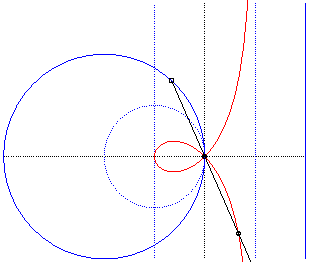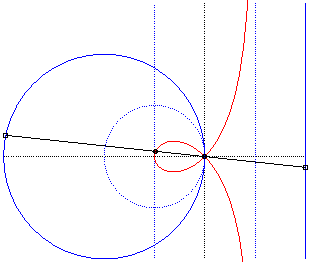The strophoid is the cissoid of the dotted circle and external line, hence also the median of the full circle and line, homothetic images of the previous ones.

    - the pedal of a parabola with respect to the foot of its directrix (here the parabola with vertex F and directrix the axis of the strophoid (equation ), with respect to the foot O of this axis).

Therefore, the right strophoid is the envelope of the circles with diameters joining O to a point on the parabola. In other words it is a cyclic curve with deferent (or initial curve) a parabola, a radius of inversion equal to zero and a pole at the foot of the directrix of the parabola.

    - the inverse of a rectangular hyperbola with respect to one of its vertices (here the rectangular hyperbola with vertices O and F (equation ), with respect to O).

- by the Newton set-square method:	- as a kieroid

The right strophoid is also:
    - a special case of nodal curve (cf. the second polar equation).
    - a special case of cubical hyperbola (cf. the Cartesian equation)

- a special case of Maclaurin sectrix, hence the construction with 2 lines in uniform rotation, one of which going twice as fast as the other. Application: the locus of the centre of the circle inscribed in the triangle ABC when C describes the circle with centre A and radius AB is a right strophoid.

    - the stereographic projection of Viviani's window.

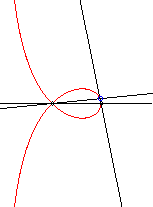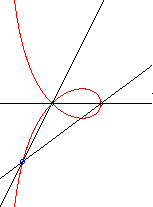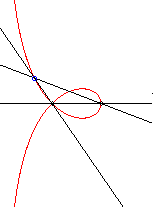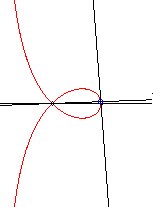Finally, it has a mechanical definition as a curve of the tightrope walker:

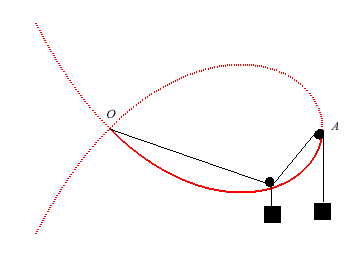A tightrope walker walks on a rope attached to a fixed point O, passing by a pulley A located at the same height than the attached end, and tightened by a counterweight attached to the other end, the weight of the walker being equal to that of the counterweight.

© Robert FERRÉOL 2024