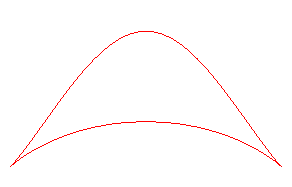
Bicorn

BICORN

Curve studied by Sylvester in 1864, Cayley in 1867 and G. de Longchamps in 1897.
Name given by Sylvester.
Other name : cocked hat curve.

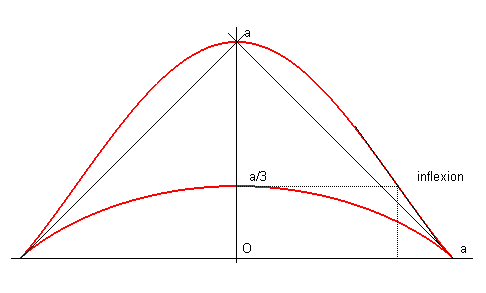Cartesian equation:

.
Cartesian parametrization:

.
Area:

.
Rational quartic, circular curve.

First construction (Charlotte Scott, Intermédiaire des mathématiciens, 1896, p. 250) Let (C) and (C') be two tangent circles, of centres O and O' and of radius a; N be a point describing (C'). The bicorn is the locus of the intersection points between the line parallel to (OO') passing through N and the polar of N with respect to the circle (C).
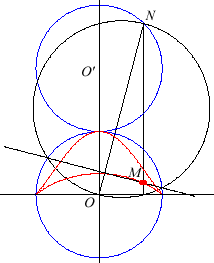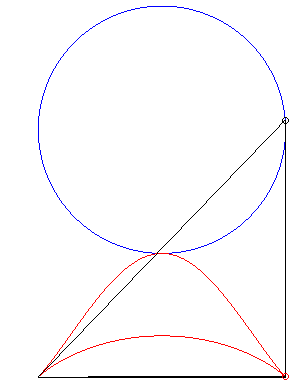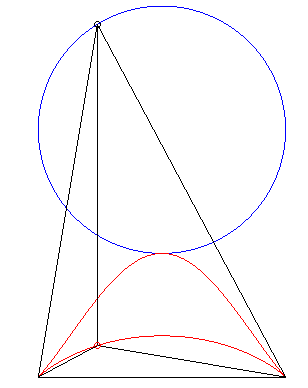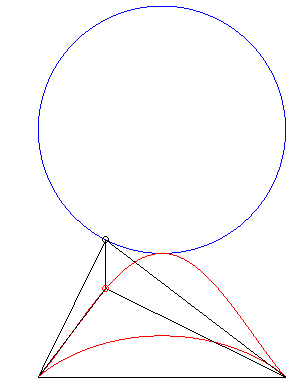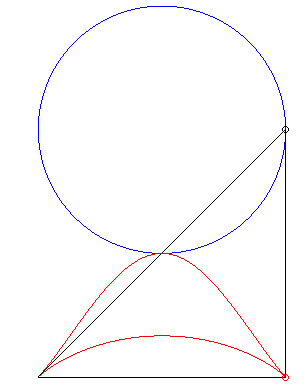
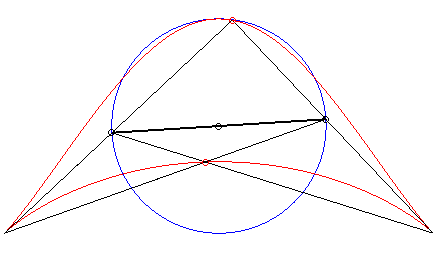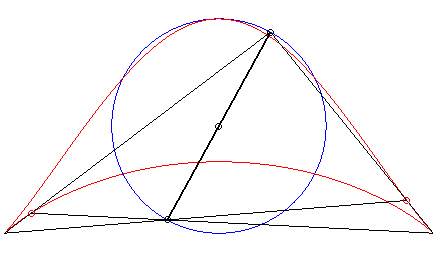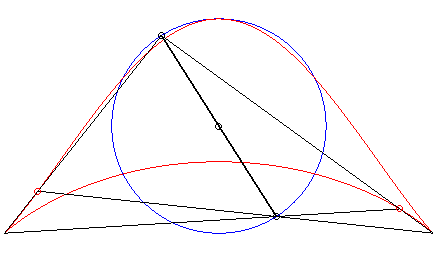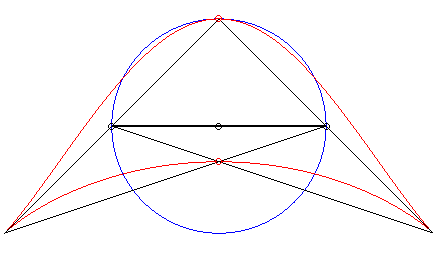
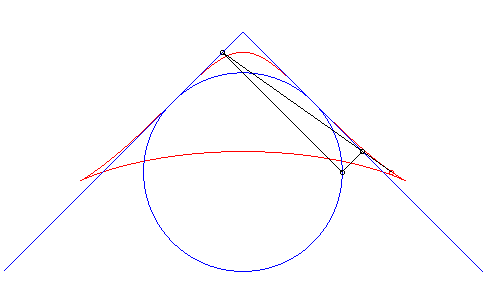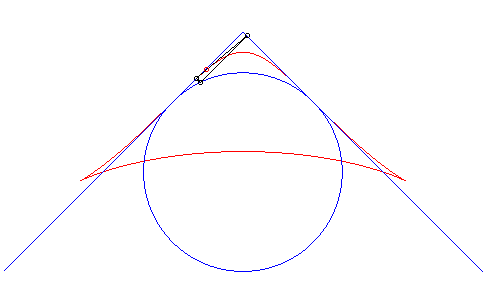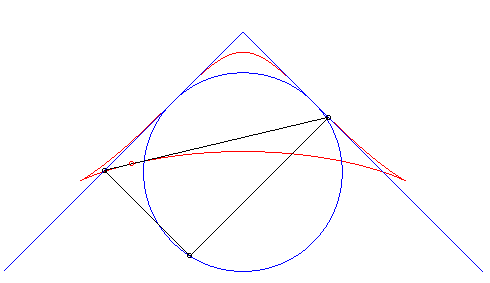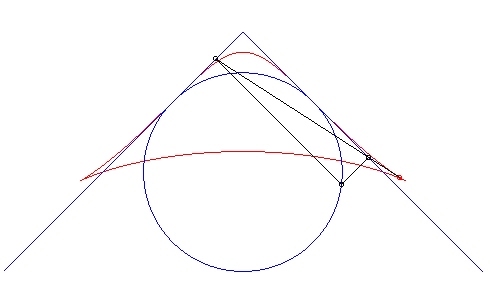
Second construction (G. de Longchamps, JMS, 1897) Given two fixed points A(a, 0) and B(–a, 0), a circle (C) of centre C(b, c) and radius r, with a current point P, the parametrization of the locus of the orthocentre H of the triangle ABP is ; when , we get the bicorn. Note: when a = b = c = 0, we get the Kappa curve, when , we get the right strophoid., and when we get the Delanges trisectrix.
Third construction (V. Jerabek, mathesis, 1912). Given two fixed points A(a, 0) and B(–a, 0), a circle (C) of centre C(0, b) and radius c, and a variable diameter [PQ] of the circle (C), the parametrization of the locus of the intersection points of the lines (AP) and (BQ) (or (AQ) and (BP) ) is ; when , we get the bicorn. If M and N are the intersection points of the lines (AP) and (BQ) and the lines (AQ) and (BP), the line (MN) envelopes a right cissoid. It is possible to generalize by considering the two points P and Q as linked to a moving plane overlying a fixed plane containing A and B ; here, the moving plane is in rotational motion around C.
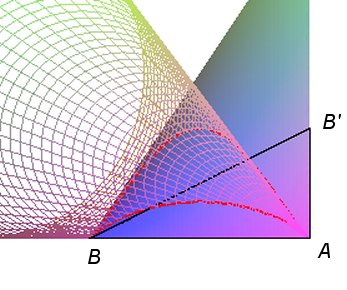
With this construction we can get the bicorn as the orthogonal projection of the intersection of an elliptic cone and a hyperbolic paraboloid (biquadratic curve). The vertex of the cone is the point A₁(a,0, h) on the vertical line passing by A, and its directrix is the circle (C). The paraboloid is defined by the 3D quadrilateral (A₁B'BB₁) where B'(a, a, 0) and B are symmetric with respect to C, and B₁(–a, 0, h) is on the vertical line passing through B.

Another characterization (Roland Deaux, 1945): the bicorn is the locus of the centre of the incircle of a triangle two vertices of which are fixed and the perimeter of which equals the sum of the radiuses of its excircles.

A point M of a circle can be projected on two points P and Q on two tangents to the circle perpendicular to one another. When M describes the circle, the line (PQ) envelopes a quartic with two cusps whose parametrization is, up to similarity, given by .
But it is not a bicorn because the tangents at the cusps do not pass through the vertex.

The mathematical bicorn is closer to the British army's cocked hat... ...than to the one owned by students of Ecole Polytechnique...

.

© Service audiovisuel École Polytechnique

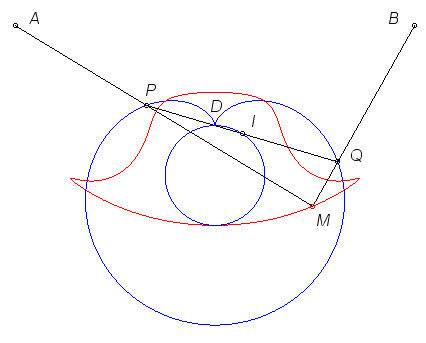
... Henri Lazennec applied Jerabek's construction and replaced the circle by a cardioid.
He considers the points A(–4, 0), B(4, 0), C(0, –3), D(0, –2).
The extremities of the line segment [PQ] of fixed length 4, passing through D and whose middle I describes the circle of centre C and radius 1, describe a cardioid with cusp D.
When [PQ] turns on the cardioid, the intersection point M of (AP) and (BQ) describes a curve looking like the bicorn, with its tips upside-down.
Parametrization: .

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The mathematical bicorn is closer to the British army's cocked hat...	...than to the one owned by students of Ecole Polytechnique...
	. © Service audiovisuel École Polytechnique
... Henri Lazennec applied Jerabek's construction and replaced the circle by a cardioid. He considers the points A(–4, 0), B(4, 0), C(0, –3), D(0, –2). The extremities of the line segment [PQ] of fixed length 4, passing through D and whose middle I describes the circle of centre C and radius 1, describe a cardioid with cusp D. When [PQ] turns on the cardioid, the intersection point M of (AP) and (BQ) describes a curve looking like the bicorn, with its tips upside-down. Parametrization: .