DELANGES TRISECTRIX AND SECTRIX
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
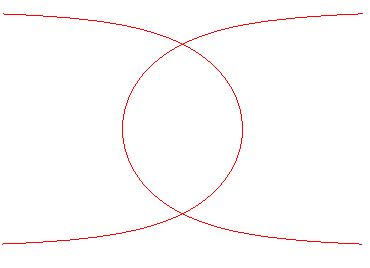
DELANGES TRISECTRIX AND SECTRIX

| Curve studied by Delanges in 1783. |
 |
Polar equation: Cartesian parametrization: (t = q / 2). Cartesian equation: Rational circular quartic. |
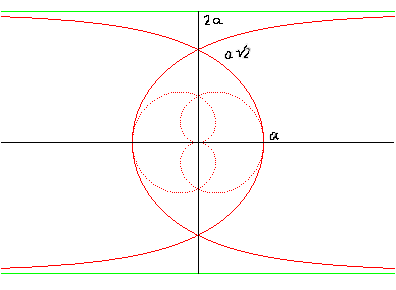
| Given a circle (C) (here, the circle with centre O and radius 2a) and a line (D0) passing through the centre of the circle (here Ox), the Delanges trisectrix is the locus of the point M on a variable line (D) passing through O such that the line parallel to D passing through M cuts (C) at N in such a way that (ON) is a bisector of (D0) and (D). |
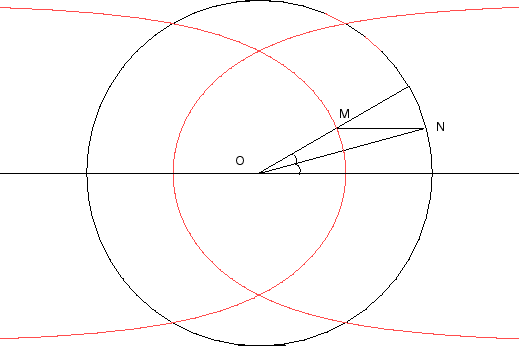 |
| Construction equivalent to the previous one: the circle
(C) has radius a, A is a fixed point of (C),
N
is a variable point. The symmetry of the line (OA) with respect to (ON)
intersects the tangent to the circle at N at point M |
 |
| The Delanges trisectrix is the locus of the orthocentre
of a triangle with a fixed side the opposite vertex of which describes
a circle centred on the middle of the side, with radius the length of the
side multiplied by See a similar construction for the bicorn, the right strophoid, and the Kappa. |
 |
The Delanges trisectrix is a special case of Cotes'
spiral.
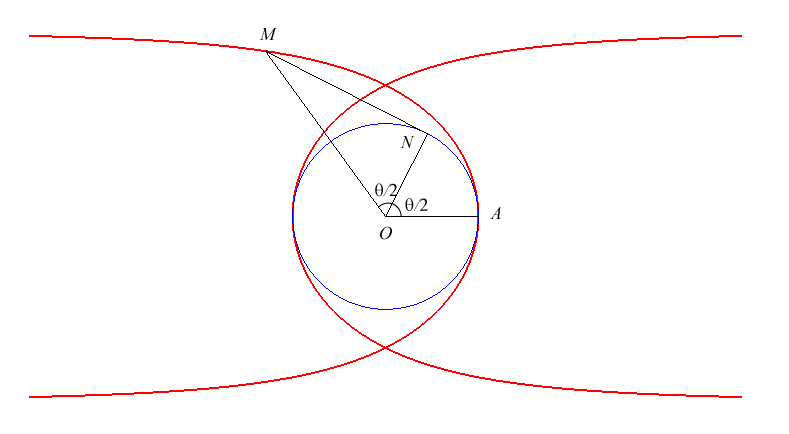
| The construction opposite shows the property of trisection: the angle MOP is the third of AOP. |
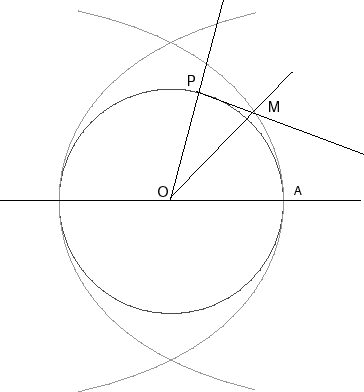 |
Its inverse curve with respect to O is the Dürer folium, which is, therefore, also a trisectrix.
Furthermore, the same construction shows that the curve
with equation
is an (n + 1)-sectrix, that can be called "Delanges sectrix".
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2024