Differential equation:  with e = 1 for the elliptic roulette (ellipse with semi-axes a and b (a > b)),  e = –1 for the hyperbolic roulette (hyperbola with semi-axes a and b), . Curvilinear abscissa: , hence the normal: . Radius of curvature:  (such that , the mean curvature of the associated surface of Delaunay). Cartesian parametrization in the elliptic case: where , e = c / a and E is the elliptic function of the second kind. Curvilinear abscissa: . Length on a period: . Area between the curve and Ox, on a period: . Cartesian parametrization in the hyperbolic case: where , e = c / a and F is the elliptic function of the first kind. Curvilinear abscissa: . Length on a period: .

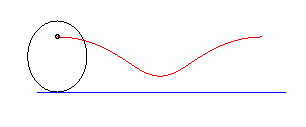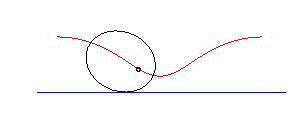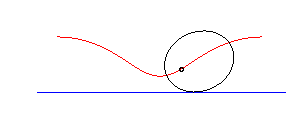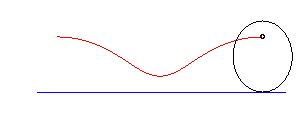
The Delaunay roulette is the locus of one of the foci of a conic rolling without slipping on a line. It is elliptic, parabolic, or hyperbolic, depending on whether the conic is an ellipse, a parabola, or a hyperbola.
 

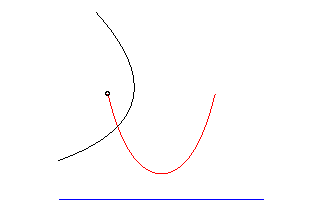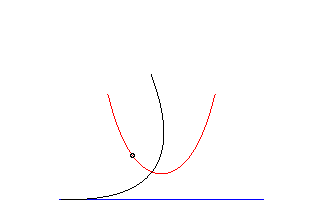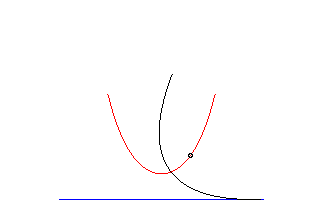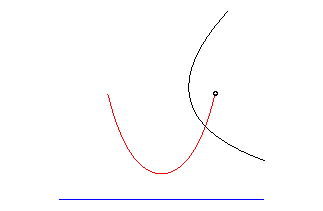
The parabolic roulette of Delaunay is none other than the catenary.

With Ox as the rolling axis, the Delaunay roulette is a curve oscillating between the lines  and . The line y = b is where can be found: in the elliptic case, inflection points with a slope equal to ; and points with vertical tangent in the hyperbolic case. The period of y as a function of x is given by the elliptic integral l(2p); it is the length of the ellipse in the elliptic case.

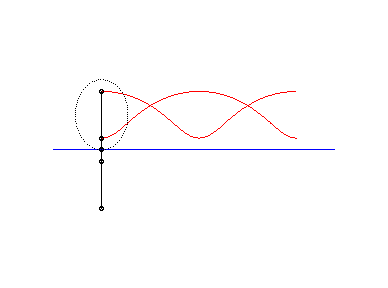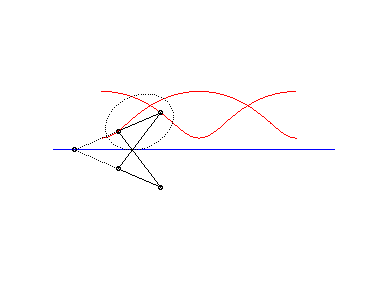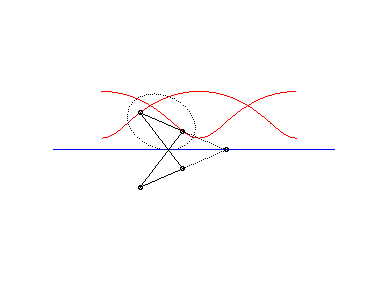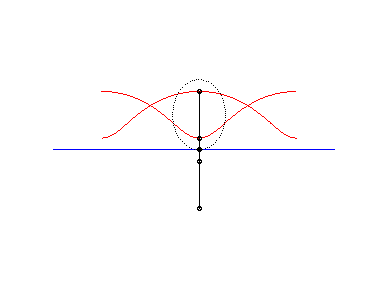
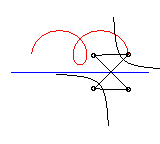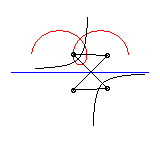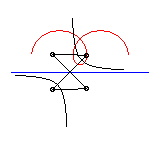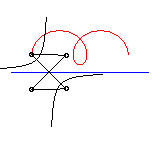
The following ingenious articulated mechanism can trace Delaunay roulettes:
  We begin with an articulated quadrangle FF'GG' with sides FF' = 2c et FG' = 2a. The lines (FG') and (F'G) intersect at P and the lines (FF') and (GG') intersect at Q. The points P and Q are constrained to move on the rolling line. We place casters on the arms (FG') and (FG) so that their movement is constantly perpendicular to themselves. F and F' are then the foci of the conic, tangent at P to the rolling line.
 
 

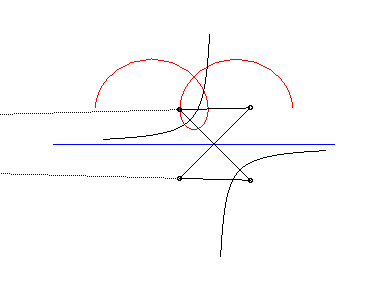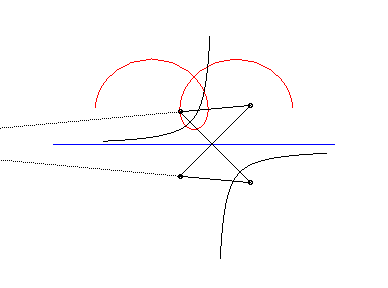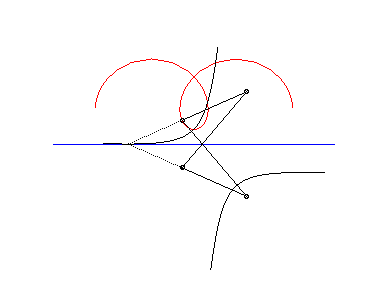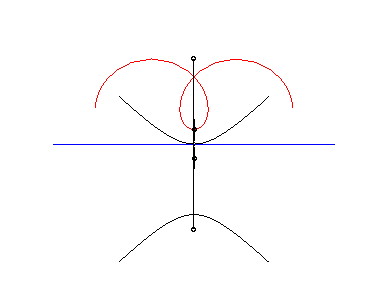This animation shows that, in the parabolic case, the directrix of the parabola envelopes the symmetric catenary about the rolling axis. This directrix cuts the rolling line at the same point than the tangent to the roulette at the corresponding point.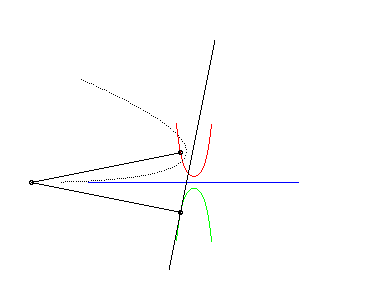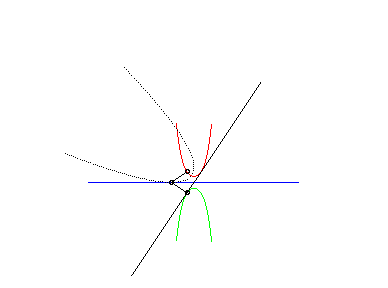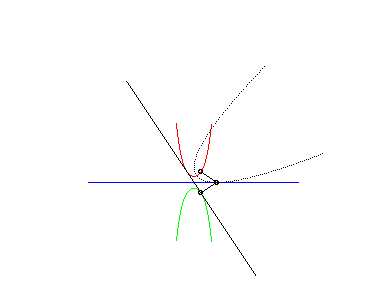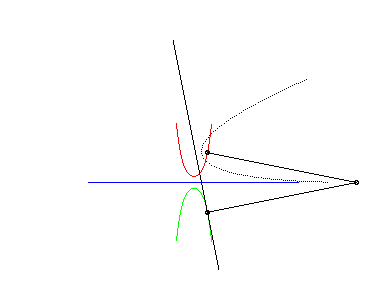

These curves were considered by Delaunay because of their property of being the only meridians of the surfaces of revolution with constant mean curvature, which are the Delaunay surfaces.

See also the Sturm roulettes, locus of the centre of the conic, as well as the determination of the road associated to an elliptic wheel.

Link: www.gang.umass.edu/gallery/cmc/cmcgallery0101.html

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017