Piriform quartic

PIRIFORM QUARTIC
Poire ou goutte d'eau ?

Curve studied by Wallis in 1685 and Bonnet in 1844.
From the Latin Pirum "pear".
Other names: drop of water, peg-top.

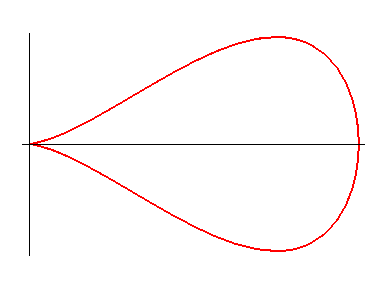Cartesian equation:

, or

.
For b = a / 2, the equation can be written:

.
Cartesian parametrization:

with

.
Rational quartic.
Area:

The 3D drop (revolution of the quartic around its axis put on Oz) has the equation : .
Volume of this drop : .

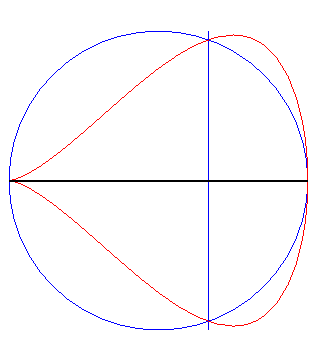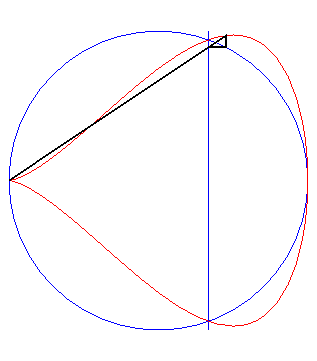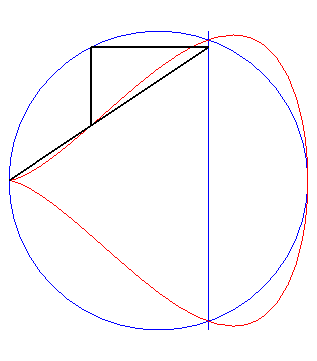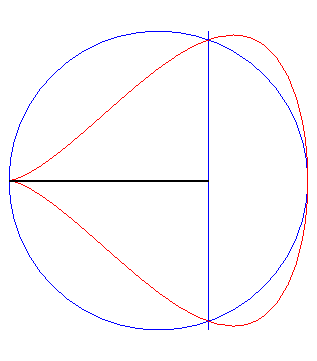
Given a point P describing the circle (C) with diameter [OA] (where A is the point with coordinates (a, 0)), let Q be the point on the line x = b with same ordinate as P. The piriform quartic is the locus of the point M on the line (OQ) with same abscissa as P.

In other words, the piriform quartics are the antihyperbolisms of the circle with respect to a point O on this circle and a line perpendicular to the diameter one end of which is O.

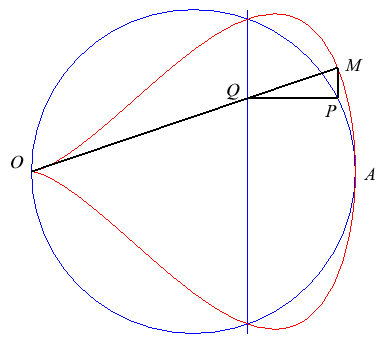Note that the piriform quartics for any value of b are images of the curve obtained when a = b by a scaling along Oy.
They are special cases of tear curves.

Up to scaling, the piriform quartic is a plane projection of the pancake curve x=cos(u),y=sin(u),z=sin(2u).

A tube with a bore shaped like a piriform quartic is a representation of the Klein bottle.

See also the double drop of water, the kieroids, and the spherical cycloids.

See also here the "true" profile of the drop of water.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra