The polar with respect to the circle with centre O and radius a of the point M0 (x0, y0) is the line with equation . If M0 is the current point on , then the current point M of the polar of  is defined by  which yields: in Cartesian coordinates, i.e.  in complex parametrization.

1) Reminder on poles and polars.

Two points M and M₀ are said to be conjugates of one another with respect to a circle (C) with centre O and radius a when the circle with diameter [M₀M] is orthogonal to (C), i.e. ; this comes from the fact that when the line (M₀M) cuts the circle at A and B, M and M₀ are harmonic conjugates with respect to [AB].

The polar of a point M₀ with respect to (C) is then the locus of the conjugates M of the point M₀ with respect to the circle, and therefore defined by the relation ; it is the line orthogonal to the line (OM₀) passing by the inverse of M₀ with respect to (C); it is also the radical axis of the circle (C) and of the circle with diameter [OM₀]. When M₀ is outside (C), it is the line joining the contact points of the tangents to the circle that pass by M₀. Conversely, a line is the polar of a unique point, called its pole.
Despite its relation to the inversion, the natural space of this transformation is not the conformal plane, but the projective plane: the polar of the point O then is the line at infinity, and the polar of a point at infinity is the line passing by O and perpendicular to the direction of the point.

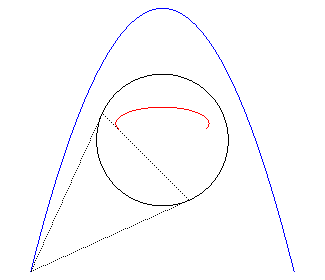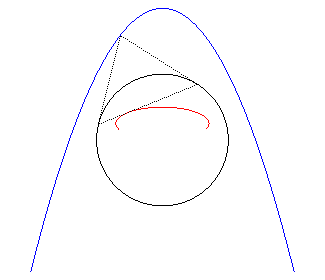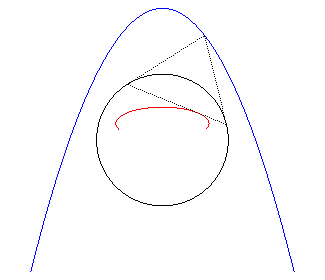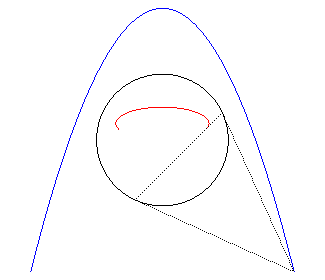
2) Definition of the polar of a curve.

The polar of a plane curve  with respect to a circle (C) (the "directrix (C)") is the envelope of the polars of the points  with respect to (C); it can be proved that it also is the set of the poles of the tangents to  with respect to (C).
 

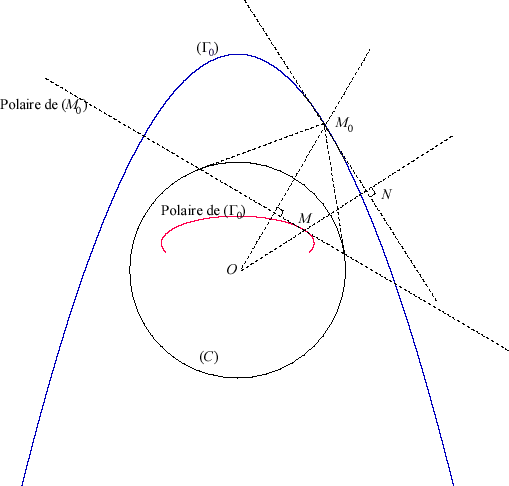The characteristic point of the polar of M0 is also the pole of the tangent to  at M0; then, it is the intersection point between the polar and the line perpendicular to this tangent passing by O. Therefore, the point N describes the pedal of , and the point M describes the inverse of the polar.

This transformation, called reciprocal polar transformation is an involution, that is, the polar of the polar is equal to the initial curve.

The inverse of the polar with respect to the same circle is none other than the pedal of the initial curve; we can sum this up with this diagram:

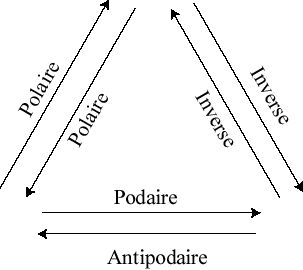
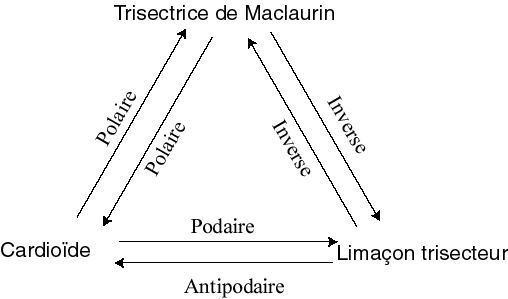
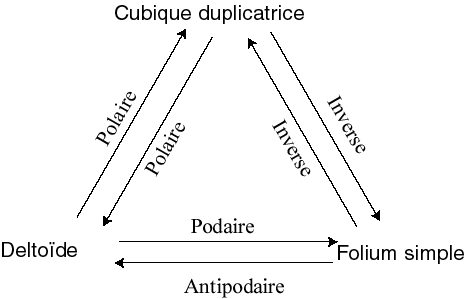
See two examples opposite:

The polar of an algebraic curve is an algebraic curve the degree of which is equal to the class of the initial curve (i.e. the degree of the tangential equation).

Examples:
 

initial curve	position of the centre of (C) with respect to the initial curve	position of the centre of (C) with respect to the polar	polar
line (polar of the point)	outside of the line	different from the point	point (pole of the line)
conic			conic
conic	focus		circle
conic	inside the conic (i.e. in a domain containing a focus)		ellipse
conic	outside the conic		hyperbola
conic	on the conic		parabola
cardioid	cuspidal point	focus at the 8/9 of the segment line joining the double point to the summit.	Tschirnhausen cubic
cardioid	centre of the conchoidal circle	focus	Maclaurin trisectrix
deltoid	centre	vertex	duplicatrix cubic
astroid	centre	centre	cross curve
centred cycloid	centre	centre	epispiral
sinusoidal spiral with parameter .	centre	centre	sinusoidal spiral with parameter .

See the 3D generalisation of these notions.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017