; ceci vient de ce que lorsque la droite (M0M)
coupe la sphère en A et B, M et M0
sont conjugués harmoniques l'un de l'autre par rapport à
[AB].
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
POLAIRE D'UNE SURFACE PAR RAPPORT A UNE SPHÈRE
Reciprocal
polar of a surface, reziproke Polare einer Fläche
1) Quelques rappels sur les pôles et polaires.
Deux points M et M0
sont dits conjugués par rapport à un sphère
(S) de centre O et de rayon
a lorsque la sphère
de diamètre [M0M]
est orthogonale à (S), ce qui se traduit par
; ceci vient de ce que lorsque la droite (M0M)
coupe la sphère en A et B, M et M0
sont conjugués harmoniques l'un de l'autre par rapport à
[AB].
Le plan polaire d’un point M0
par rapport à (S) est alors le lieu des conjugués
M
du point M0 par rapport à
la sphère, donc défini par la relation
; c’est le plan orthogonal à la droite (OM0)
passant par l’inverse de M0 par
rapport à (S) ; c’est aussi l’axe radical de la sphère
(S) et de la sphère de diamètre [OM0].
Quand M0 est extérieur à
(S), c’est le plan du cercle des points de contact des tangentes
issues de M0 à la sphère
(S). Inversement un plan est polaire d’un unique point, appelé
son pôle.
Bien que liée à l’inversion, l’espace naturel
de cette transformation n’est pas l'espace conforme 3D, mais l'espace projectif
3D : le plan polaire du point O est alors le plan de l’infini, et
le plan polaire d’un point à l’infini, le plan passant par O
et perpendiculaire à la direction du point.
2) Définition de la surface polaire d'une surface par rapport à une sphère.
La surface polaire (réciproque) d'une surface (S0) par rapport à une sphère (S) (ou de sphère directrice (S)) est l'enveloppe des plans polaires des points de (S0) par rapport à (S) ; on démontre que c'est aussi l'ensemble des pôles des plans tangents à (S0) par rapport à (S).
Cette transformation, appelée transformation par
polaires réciproques, est involutive, autrement dit, la
polaire de la polaire est égale à la surface
de départ.
L'inverse de la polaire par rapport à la même sphère n'est autre que la surface podaire de la surface de départ ; on peut résumer ceci par le diagramme :
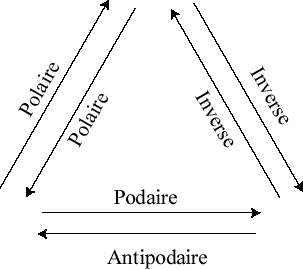
La polaire d'une surface algébrique est une surface algébrique dont le degré est égal à la classe de la courbe de départ (c'est à dire le degré de l'équation tangentielle).
3) Définition de la surface développable polaire d'une courbe par rapport à une sphère.
La surface développable polaire d'une courbe (G0) par rapport à une sphère (S) (ou de sphère directrice (S)) est l'enveloppe des plans polaires des points de (G0) par rapport à (S) ; on démontre que c'est aussi l'ensemble des pôles des plans osculateurs à (G0) par rapport à (S).
Ne pas confondre cette notion avec celle de surface
polaire d'une courbe, engendrée par les droites polaires.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2003