La polaire par rapport au cercle de centre O et de rayon a du point M0 (x0, y0) est la droite d'équation . Si M0 est le point courant d'une courbe , le point courant M de la polaire de  est défini par  ce qui donne : en cartésien, soit  en complexes.

1) Quelques (r)appels sur les pôles et polaires.

Deux points M et M₀ sont dits conjugués par rapport à un cercle (C) de centre O et de rayon a lorsque le cercle de diamètre [M₀M] est orthogonal à  (C), ce qui se traduit par  ; ceci vient de ce que lorsque la droite (M₀M) coupe le cercle en A et B, M et M₀ sont conjugués harmoniques l'un de l'autre par rapport à [AB].

La polaire d’un point M₀ par rapport à  (C) est alors le lieu des conjugués M du point  M₀ par rapport au cercle, donc défini par la relation  ; c’est la droite orthogonale à la droite (OM₀) passant par l’inverse de M₀ par rapport à (C) ; c’est aussi l’axe radical du cercle (C) et du cercle de diamètre [OM₀]. Quand M₀ est extérieur à (C), c’est la droite qui joint les points de contact des tangentes issues de M₀ au cercle (C). Inversement une droite est la polaire d’un unique point, appelé son pôle.
Bien que liée à l’inversion, l’espace naturel de cette transformation n’est pas le plan conforme, mais le plan projectif : la polaire du point O est alors la droite de l’infini, et la polaire d’un point à l’infini, la droite passant par O et perpendiculaire à la direction du point.

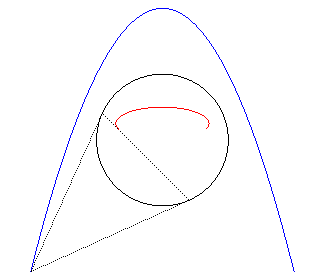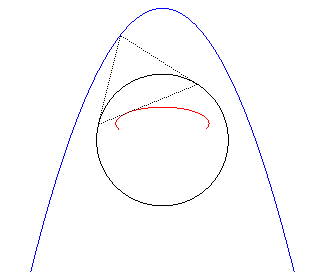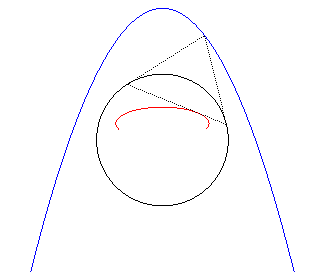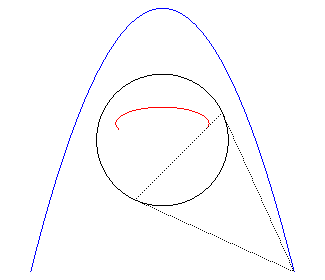
2) Définition de la polaire d'une courbe.

La polaire d'une courbe plane  par rapport à un cercle (C) (ou «de cercle directeur (C)») est l'enveloppe des polaires des points de  par rapport à (C) ; on démontre que c'est aussi l'ensemble des pôles des tangentes à  par rapport à (C).
 

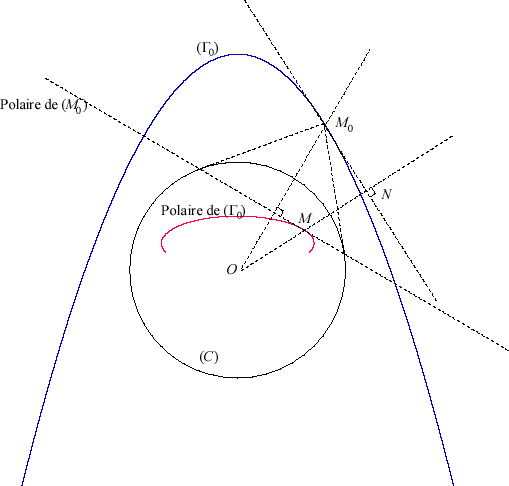Le point caractéristique de la polaire de M0 est aussi le pôle de la la tangente à  en M0 ; c'est donc le point d'intersection de la perpendiculaire à cette tangente passant par O et de la polaire. Le point N décrit donc la podaire de , et le point M, l'inverse de cette podaire.

Cette transformation, appelée transformation par polaires réciproques est involutive, autrement dit, la polaire de la polaire est égale à la courbe de départ.

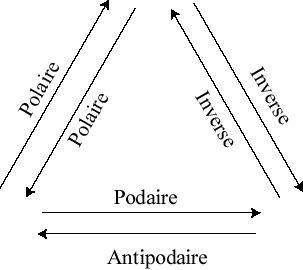
L'inverse de la polaire par rapport au même cercle n'est autre que la podaire de la courbe de départ ; on peut résumer ceci par le diagramme :

Voir deux exemples ci-contre :

La polaire d'une courbe algébrique est une courbe algébrique dont le degré est égal à la classe de la courbe de départ (c'est à dire le degré de l'équation tangentielle).

Exemples :
 

courbe de départ	position par rapport à la courbe de départ du centre de (C)	position par rapport à la polaire du centre de (C)	polaire
droite (polaire du point)	hors de la droite	différent du point	point (pôle de la droite)
conique			conique
conique	foyer		cercle
conique	à l'intérieur de la conique (i.e. dans une région contenant un foyer)		ellipse
conique	à l'extérieur de la conique		hyperbole
conique	sur la conique		parabole
cardioïde	point de rebroussement	foyer au 8/9 ème du segment joignant le point double au sommet.	cubique de Tschirnhausen
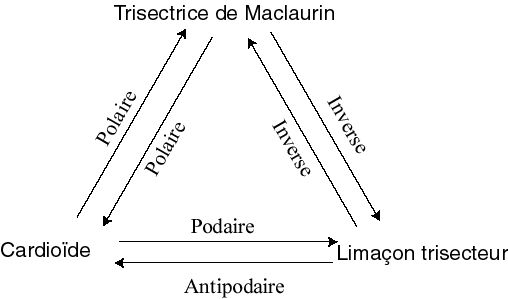
cardioïde	centre du cercle conchoïdal	foyer	trisectrice de Maclaurin
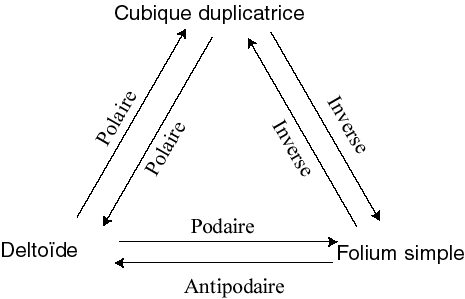
deltoïde	centre	sommet	cubique duplicatrice
astroïde	centre	centre	cruciforme
cycloïde à centre	centre	centre	épi
spirale sinusoïdale de paramètre .	centre	centre	spirale sinusoïdale de paramètre .

Voir la généralisation à la 3D de ces notions.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017