Nom donné par Loria en 1930. Autres noms : courbe à n ventres, ou courbe à n saillies ( Laboulaye, 1849), conique généralisée (Mamikon, 2012).

 

Équation polaire :  avec n réel > 0. Courbe algébrique ssi n est rationnel.

 

Les polygastéroïdes sont les inverses de conchoïdes de rosaces. Ce sont aussi les projections coniques de couronnes sinusoïdales sur un plan perpendiculaire à l'axe du cylindre, le centre étant situé sur l'axe.

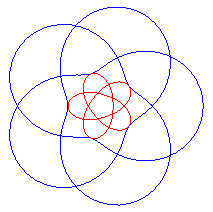
Conchoïde de rosace en bleu, polygastéroïde en rouge

Remarque : les "monogastéroïdes" (n = 1) ne sont autres que les coniques. Les polygastéroïdes sont donc aussi les transformées de Brocard des coniques par rapport à l'un de leur pôle.

La courbe est formée d'un motif de base symétrique par rapport à Ox, obtenu pour  :
 

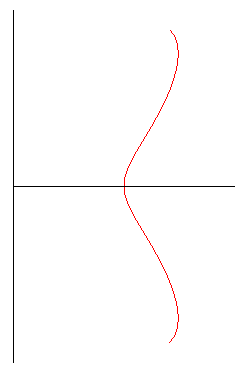
motif de base pour  e < 1

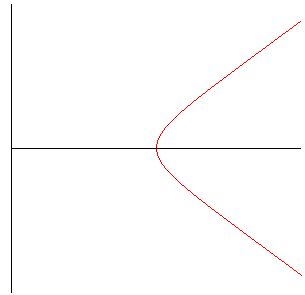
motif de base pour e = 1 (branche parabolique)

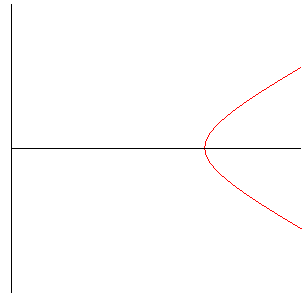
motif de base pour e > 1 (branche à asymptote)

transformé par toutes les rotations d'angle  pour k entier.
Lorsque n est rationnel de numérateur p, p rotations donnent toute la courbe.
 

Cas  e < 1 : on obtient des formes similaires à celles des conchoïde de rosaces inverses.
Pour n = p / q, la polygastéroïde de paramètre n est une des projections possibles du noeud de bonnet turc de type (p,q) ; ses p sommets externes et ses p sommets internes forment un polygone régulier, et elle possède p(q – 1) points doubles.
 

n = 1 : ellipse	n  = 2 : ovale de Booth	n = 3	n = 4	n = 5
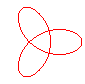
n = 1/2 :	n = 3/2 projection du noeud de trèfle	n = 5/2 projection du noeud 5.1	n = 7/2	n = 9/2
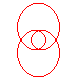
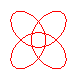
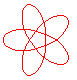
n  = 1/3	n = 2/3 projection du noeud de huit	n = 4/3 projection du noeud 8.18	n = 5/3 projection du noeud 10.123	n = 7/3
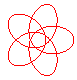
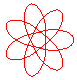
n = 1/4	n = 3/4 projection du noeud 9.40	n = 5/4	n = 7/4	n = 9/4
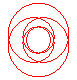
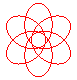
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

On peut obtenir ces courbes comme profil conjugué d'une ellipse.

Cas e = 1 ; l'équation devient  (comparer avec les épis : ) :

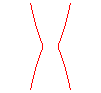
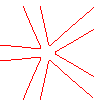
n = 1 : parabole	n  = 2 : campyle d'Eudoxe	n = 3	n = 4	n = 5
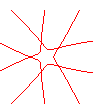
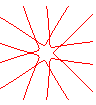
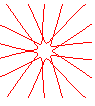
n = 1/2	n = 3/2	n = 5/2	n = 7/2	n = 9/2
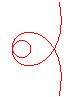
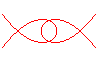
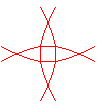
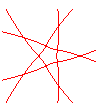
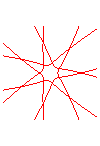
n  = 1/3	n = 2/3	n = 4/3	n = 5/3	n = 7/3
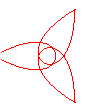
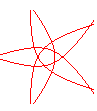
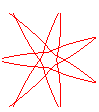
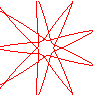
n = 1/4	n = 3/4	n = 5/4	n = 7/4	n = 9/4
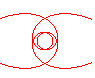
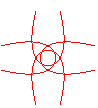
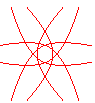
n = 1/5	n = 2/5	n = 3/5	n = 4/5	n = 6/5

Cas e > 1 :

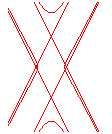
n = 1 : hyperbole	n  = 2
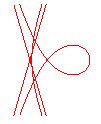
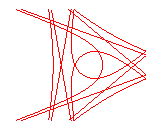
n = 1/2	n = 3/4

Les polygastéroïdes sont les développements plans des sections planes du cône de révolution.
Si l'on enroule le plan de la conique en un cône de sommet O et de demi-angle au sommet , d'axe Oz, la projection sur xOy de cette conique enroulée est la polygastéroïde : , ce qui fournit une construction de ces dernières dans le cas n < 1.

On peut obtenir ces courbes comme profil conjugué d'une droite.

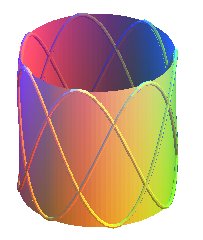
Les développées des tractoires de cercle ainsi que les projections sur le plan de symétrie des loxodromies du tore ouvert sont des polygastéroïdes.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2024