Tractoire de cercle

TRACTOIRE DE CERCLE
Tractory of a circle, Kreisschleppkurve

Courbe étudiée par Bordoni en 1820.
Autre nom : tractrice de cercle.
Animations cyclistes réalisées par Alain Esculier, en voir d'autres sur son site.
Voir gomez texeira II p 94 , loria 2d p. 220 et loria 3d p. 82

Équation différentielle cartésienne :

.
Équation différentielle polaire :

où

.
Équation polaire :
- Cas 0 < a < R (laisse inférieure au rayon) :
Branche interne :

Branche externe :

- Cas a > R (laisse supérieure au rayon) :

Voir la définition à tractoire.

Lorsque la "laisse" est égale au rayon du cercle, on obtient la spirale tractrice dont le centre du cercle est point asymptote.

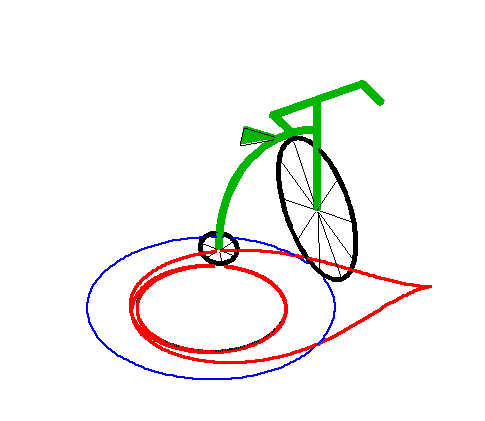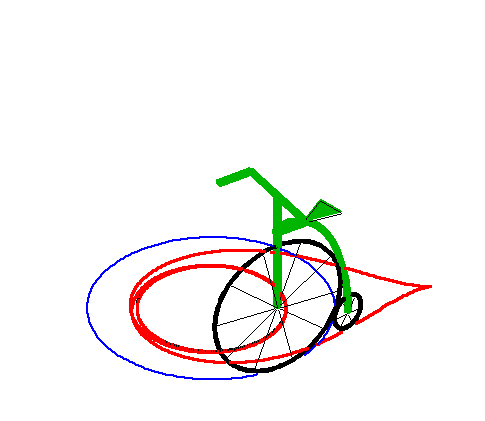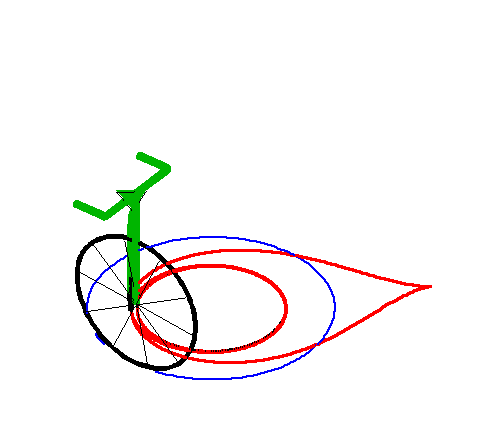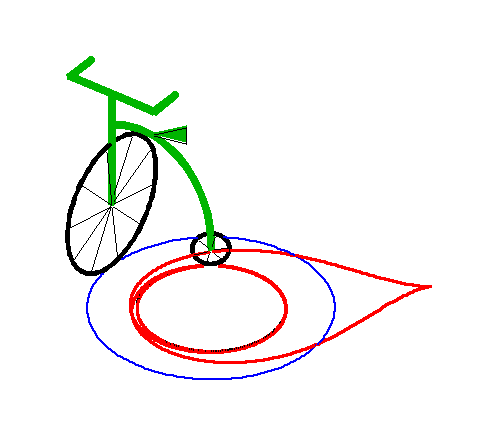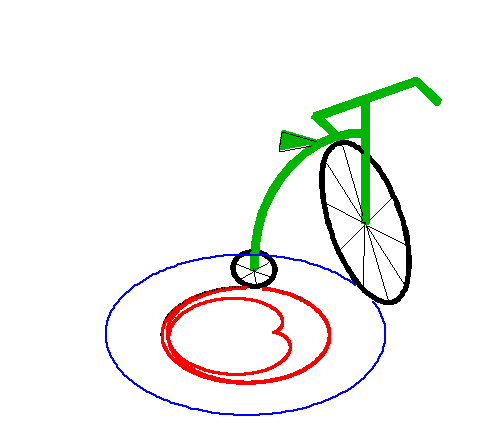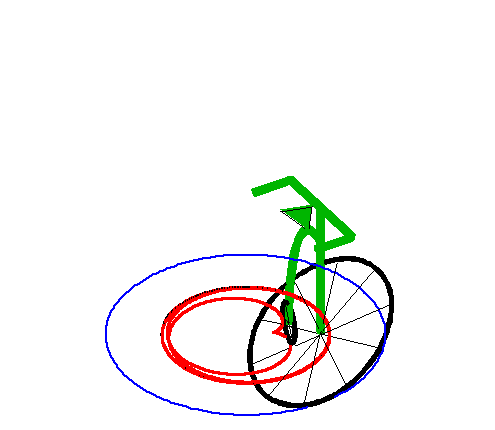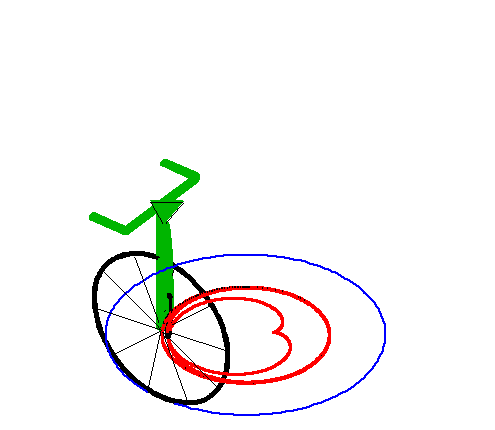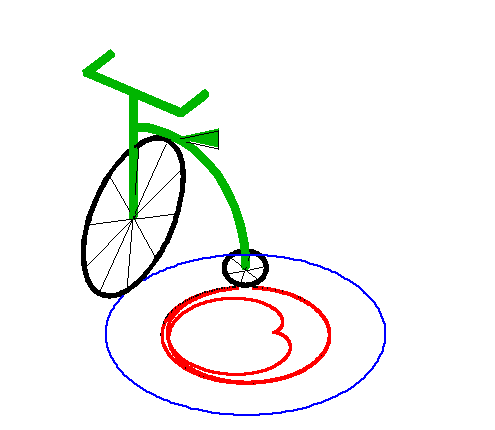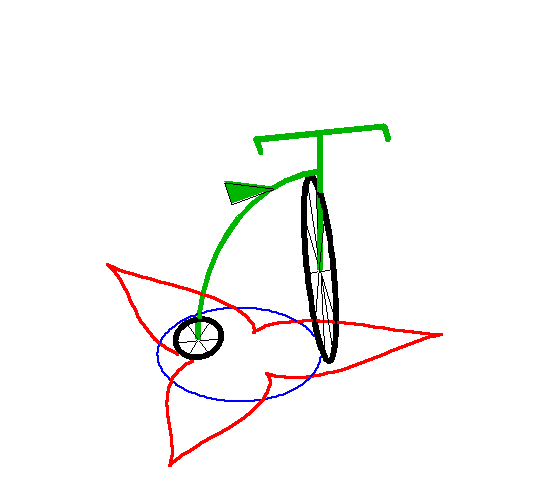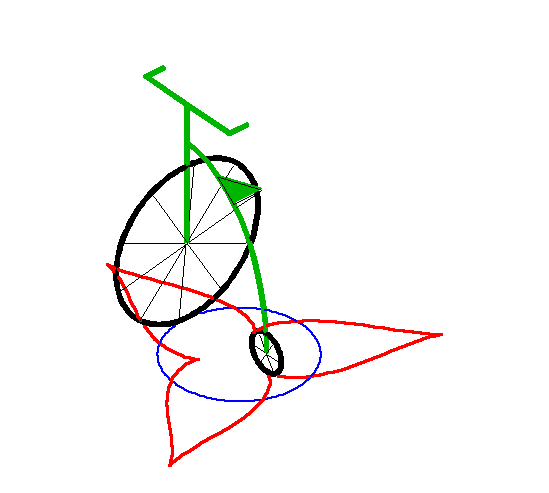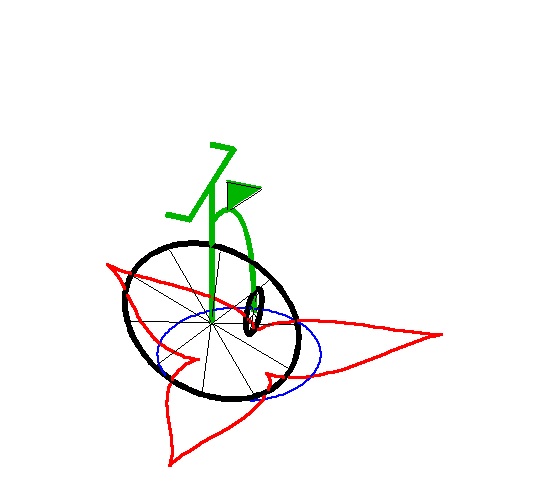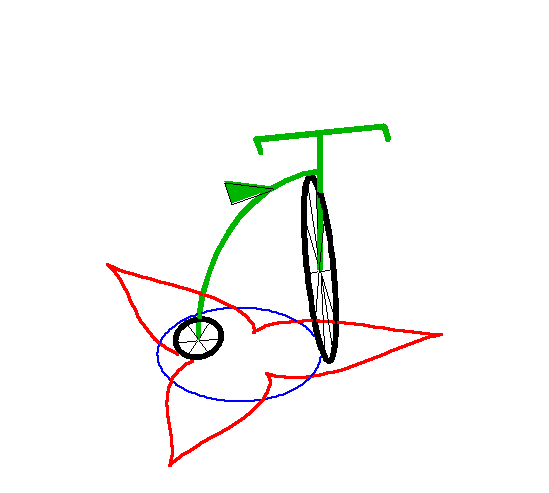
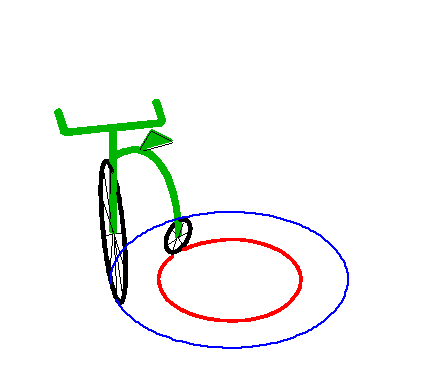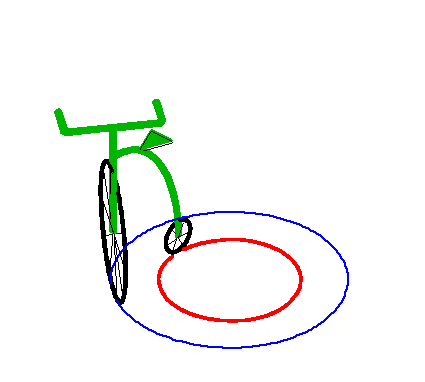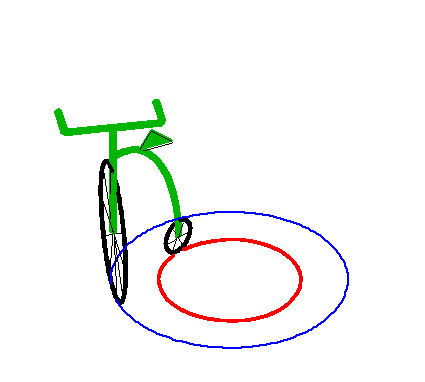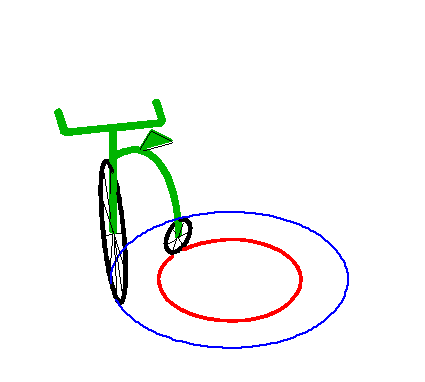
Lorsque la laisse a est strictement inférieure au rayon R du cercle, la courbe possède deux branches asymptotes au cercle de rayon ; ci dessus, animation avec la branche extérieure au cercle asymptote. Ci-dessus, avec la branche intérieure.

Ce cercle asymptote est lui-même une tractoire particulière, comme on le voit à droite.
Ceci correspond au cas d'un véhicule en mouvement avec un l'angle de braquage fixe.

Lorsque la laisse est strictement supérieure au rayon du cercle, on
obtient une courbe ayant une succession de points de rebroussements.
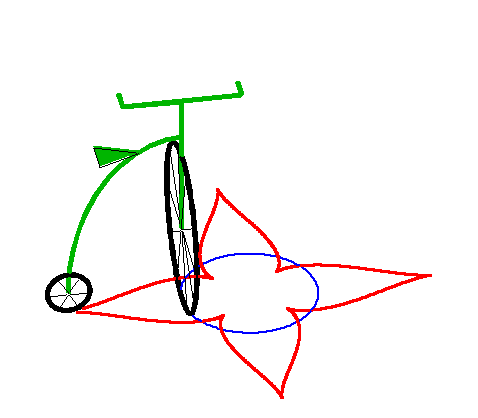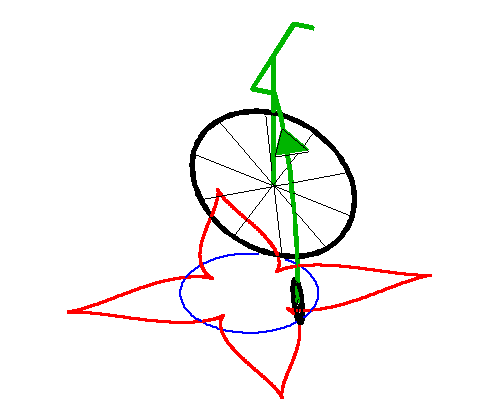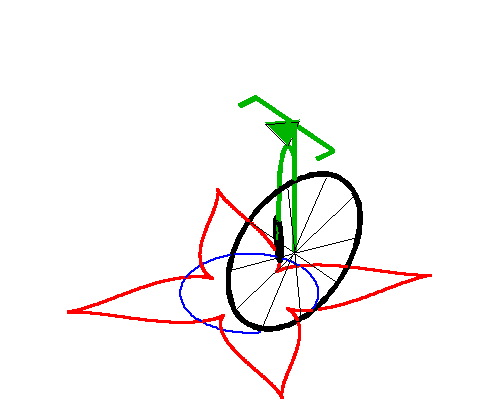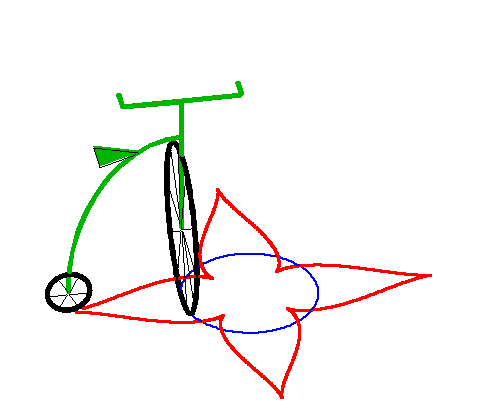Cette courbe est alors fermée ssi est rationnel : voir un exemple ci-contre et deux autres en haut de la page.

Si l'on fait glisser une tractoire de cercle sur une droite fixe en un point fixe, le pôle de la tractoire reste à distance constante de l'extrémité de la laisse et décrit donc un cercle dans le point fixe ; les tractoires de cercle sont donc solution du problème de la glissette circulaire (voir une figure dans le cas de la spirale tractrice).
Les développées des tractoires de cercle, qui sont des polygasteroïdes, sont donc solutions du problème de la roulette circulaire (voir à courbe de Catalan).

Regarder www.cabri.net/abracadabri/Courbes/Tract/Tract2b.html

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres


Lorsque la laisse a est strictement inférieure au rayon R du cercle, la courbe possède deux branches asymptotes au cercle de rayon ; ci dessus, animation avec la branche extérieure au cercle asymptote.	Ci-dessus, avec la branche intérieure.
Ce cercle asymptote est lui-même une tractoire particulière, comme on le voit à droite. Ceci correspond au cas d'un véhicule en mouvement avec un l'angle de braquage fixe.
Lorsque la laisse est strictement supérieure au rayon du cercle, on obtient une courbe ayant une succession de points de rebroussements. Cette courbe est alors fermée ssi est rationnel : voir un exemple ci-contre et deux autres en haut de la page.