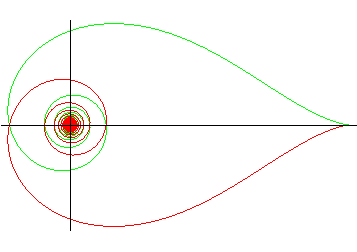
Équation différentielle : 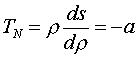. Paramétrisation polaire : 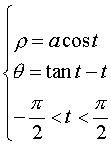 (remarquer la similitude avec la paramétrisation de la tractrice). Équation polaire : . Courbe transcendante. Angle tangentiel polaire : . Abscisse curviligne : . Rayon de courbure : . Équation intrinsèque 1 : .

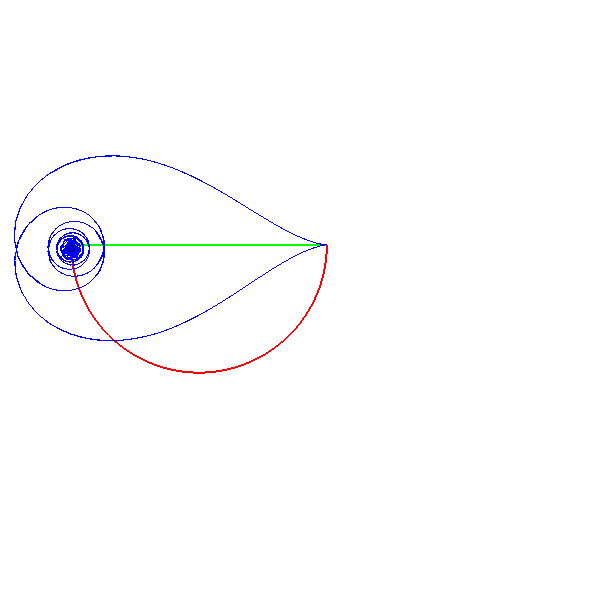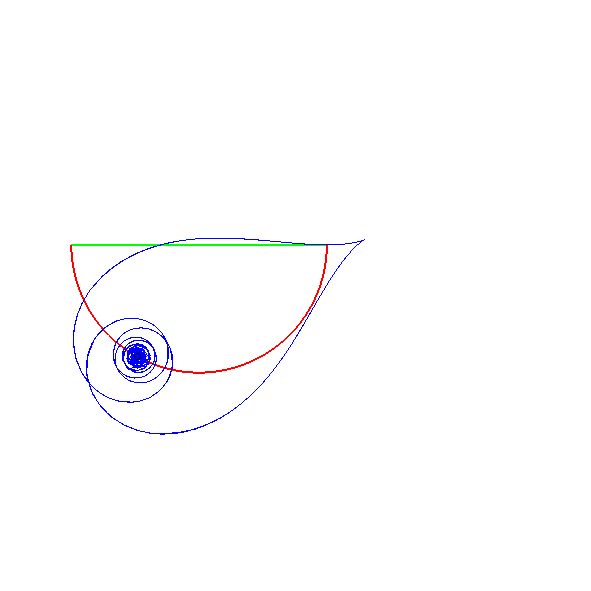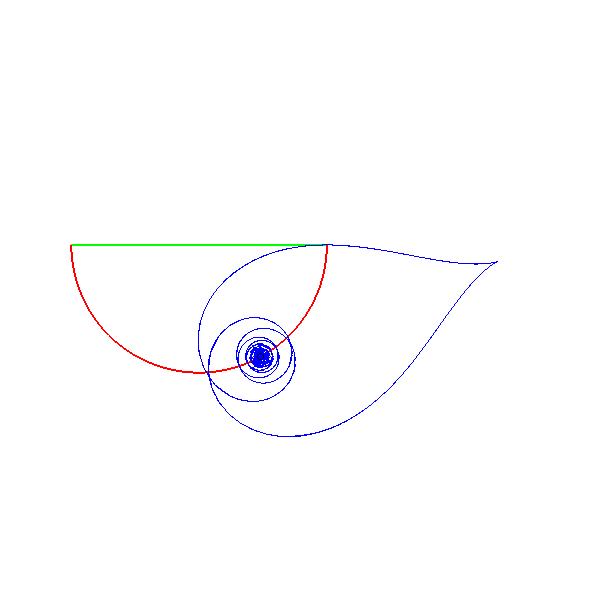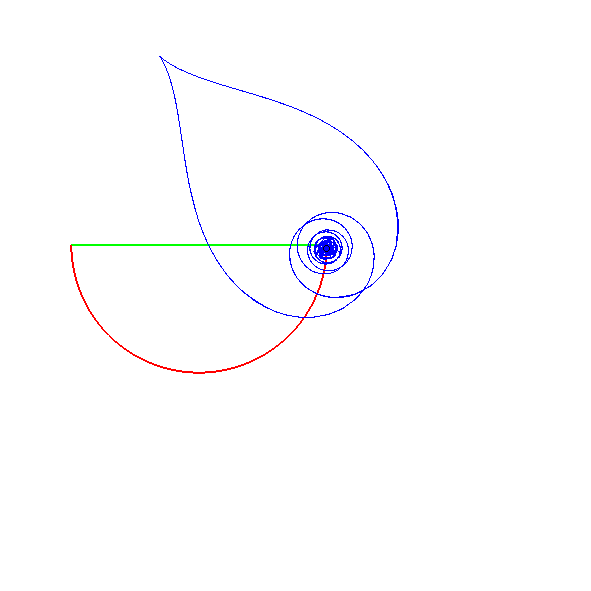
La spirale tractrice est la courbe à tangente polaire constante (alors que la tractrice tout court, est la courbe à tangente cartésienne constante).
 

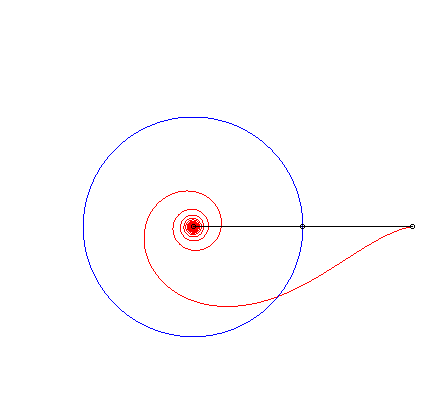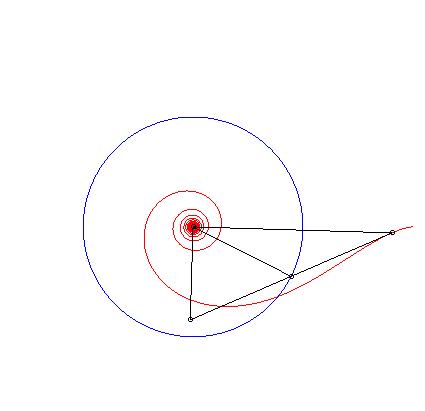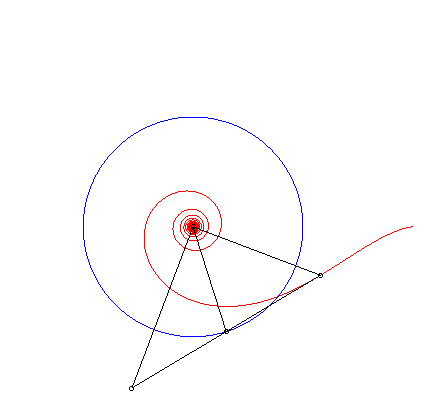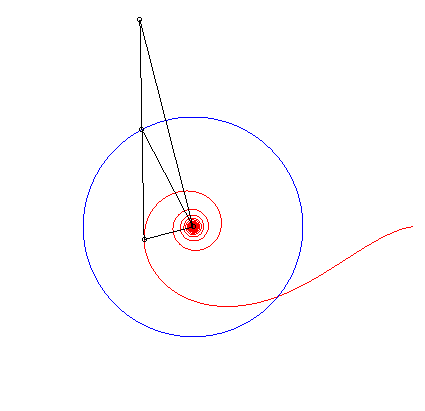
Le milieu de la tangente polaire , (qui est l'hypothénuse du triangle ) décrit donc le cercle de centre O et de rayon a/2, ce qui fait que la spirale tractrice est une tractoire de cercle, lorsque la laisse est égale au rayon du cercle.

Elle est aussi l'inverse de la développante de cercle par rapport à son centre, ainsi que l' antipodaire de la spirale hyperbolique par rapport à son centre.
 
 

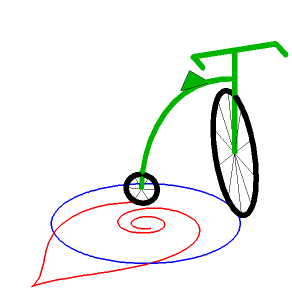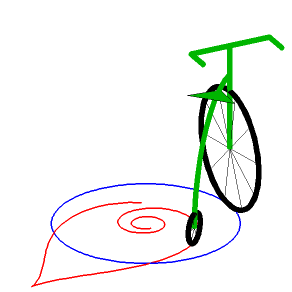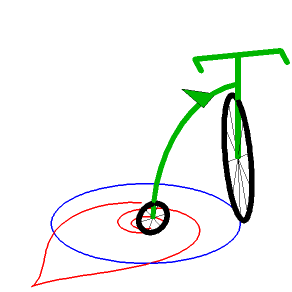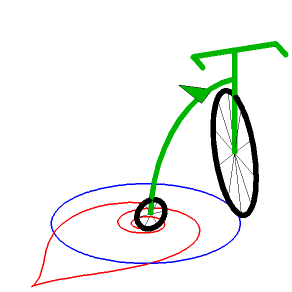
Lorsque la spirale tractrice roule sur une tractrice, de sorte que les points de rebroussement coïncident, le pôle décrit une droite (voir aussi à couple roue-route).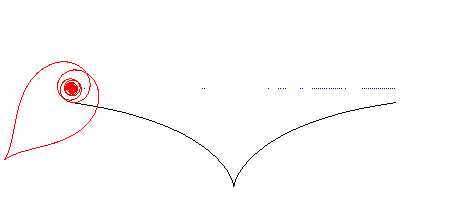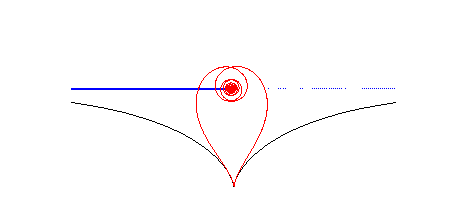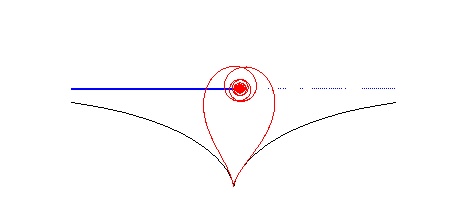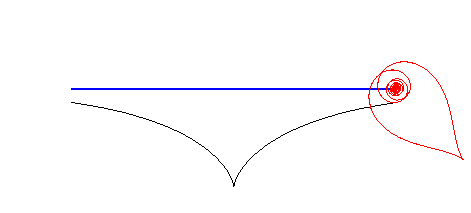

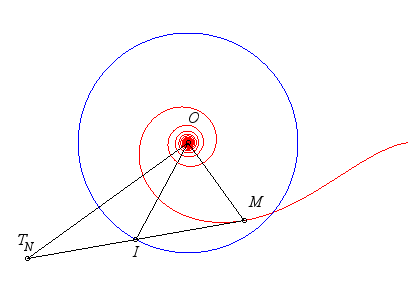Si dans la figure ci-dessus représentant la tangente polaire constante, on se place dans un repère lié à M et I, la longueur OI étant constante, le mouvement relatif de O autour de I est circulaire. Autrement dit, lorsque la spirale tractrice glisse sur une droite en un point fixe, son pôle décrit un cercle (cf. à droite). Elle est donc solution du problème de la glissette circulaire. Cette propriété a été utilisée pour déterminer la forme à donner aux tiges qui dirigent les vannes de certains canaux. Voir aussi la courbe de Catalan, développée de la spirale tractrice, qui est donc solution du problème de la roulette circulaire.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2012