SPIRALE HYPERBOLIQUE
Reciprocal
spiral, hyperbolische Spirale
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SPIRALE HYPERBOLIQUE
Reciprocal
spiral, hyperbolische Spirale

| Courbe étudiée par P. Nicolas en 1696, Varignon en 1704, Bernoulli en 1710 et Cotes en 1722. |
| Équation polaire : Abscisse curviligne : Rayon de courbure : Courbe transcendante. |
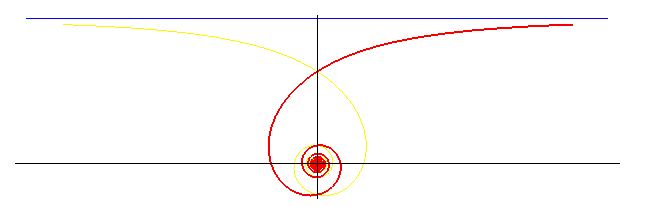
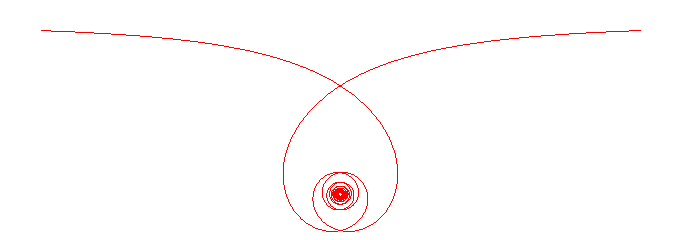
Comme la spirale logarithmique, elle possède une branche en spirale avec point asymptote, mais, au contraire de celle de la spirale logarithmique, sa longueur est infinie.
CNS : courbe dont la sous-tangente polaire est constante.
On l'obtient également comme
- inverse de la
spirale
d’Archimède
- orthocaustique
de la
spirale tractrice
par rapport au centre.
- projection conique plane (le centre de projection se
trouvant sur l'axe et le plan de projection perpendiculaire à cet
axe) d'une hélice
circulaire (théorème de Théodore Olivier).
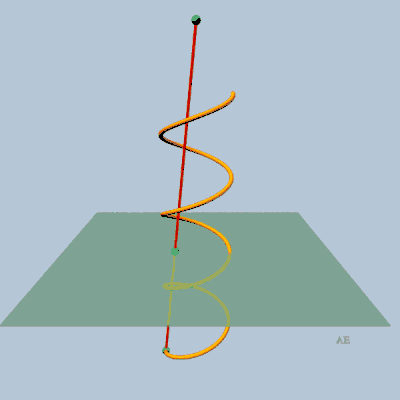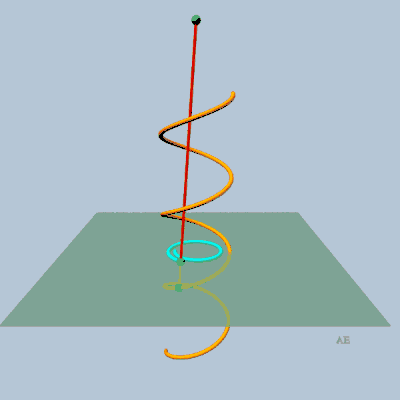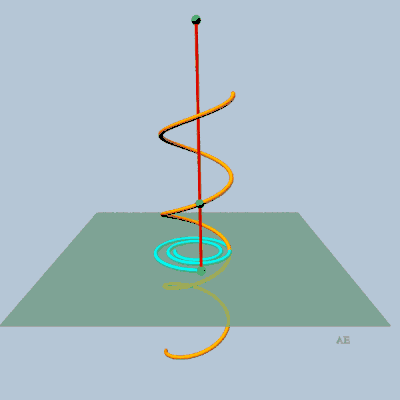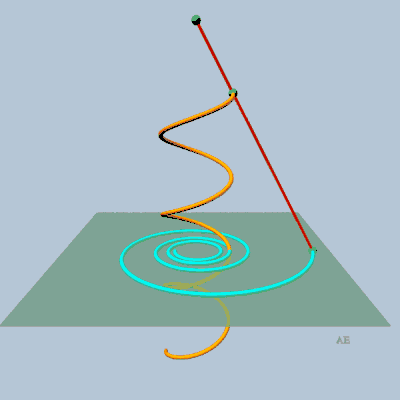 |
C'est la raison pour laquelle la perspective plongeante
d'un escalier en colimaçon est une spirale hyperbolique.
Voir aussi cette page de Gérard Lavau. |
 |
La courbe permettant de déterminer les points de
départ des coureurs sur un stade circulaire est une spirale hyperbolique
:
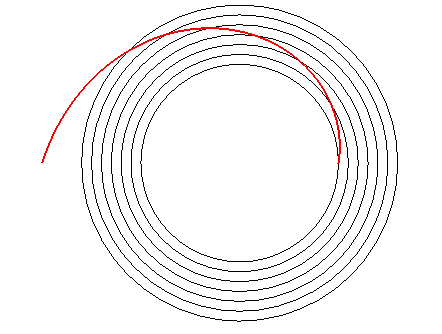
|
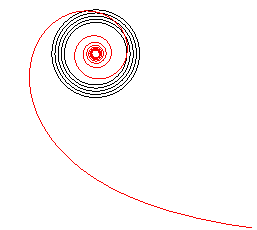 |
Lorsqu'on fait rouler une spirale hyperbolique sur une droite, son pôle décrit une tractrice, tandis que si on la fait rouler sur une logarithmique, son pôle décrit une droite.
La spirale hyperbolique est solution du problème
consistant à déterminer les trajectoires dans le vide d'un
point matériel soumis à une force centrée sur O
proportionnelle à
(cette force est d'après la formule de Binet proportionnelle à
qui vaut ici
,
avec
)
; les autres solutions sont les épis
et les spirales de Poinsot, voir
ce
lien.
Voir aussi la spirale conique hyperbolique, et comparer avec la spirale SiCi.
La spirale hyperbolique ne fait-elle pas penser à la queue d'un caméléon ?

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2018