Si M0 est le point courant de 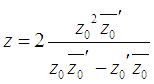, le point courant M de l'antipodaire par rapport à O est défini par  ce qui donne  : en coordonnées cartésiennes,  en complexes, et en coordonnées polaires, avec  ; on a  (voir les notations).

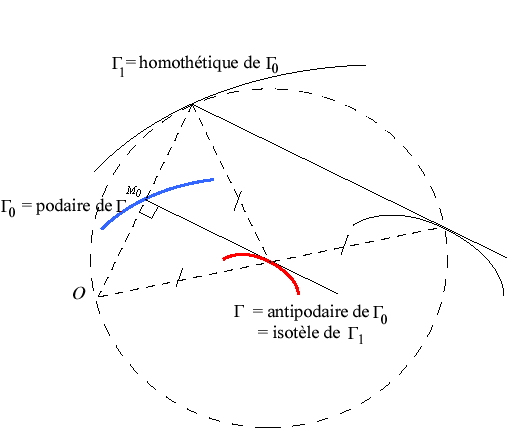
L'antipodaire d'une courbe par rapport à un point O est la courbe dont la podaire est la courbe de départ. Voir au bas de cette page une interprétation cinématique de cette définition.
 

L'antipodaire d'une courbe  par rapport à O est donc l'enveloppe des perpendiculaires en M aux droites (OM), M décrivant , d'où le nom équivalent d'orthocaustique. L'antipodaire est aussi la courbe d'équidistance entre O et l'homothétique de rapport 2 de  par rapport à O, dénommée de ce point de vue l'isotèle de cette courbe.
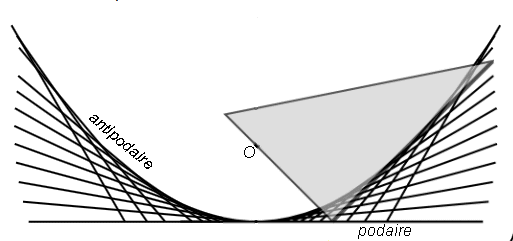
Si le sommet d'une équerre décrit la courbe de départ, et un coté est astreint à passer par O, l'autre côté enveloppe l'antipodaire. Remarque : les points du côté de l'équerre passant par O décrivent des conchoïdes de la courbe de départ, et les points de l'autre côté, des isoconchoïdes. Voir à glissette.

L'antipodaire par rapport à un point O est aussi la polaire de l'inverse, en choisissant un cercle quelconque centré en O.

Exemples :
    - les antipodaires de droite sont les paraboles (foyer en O, la droite de départ étant la tangente au sommet de la parabole)
    - les antipodaires de cercle sont les ellipses ou les hyperboles suivant que O est à l'intérieur ou à l'extérieur du cercle (foyer en O, le cercle de départ étant le cercle principal de la conique) ; lorsque O est sur le cercle, l'antipodaire se réduit au point diamétralement opposé à O.
    - l'antipodaire d'une parabole par rapport à son foyer est la cubique de Tschirnhausen
    - l'antipodaire d’une ellipse par rapport à son centre est la courbe de Talbot.
    - l'antipodaire de la développante de cercle par rapport à son centre est la caustique inverse de cercle.
 

Voir d’autres exemples à podaire !
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2012