Nom maison.

 

Pour des données A(0, a), B(0, –a), AP = BQ = 2b, AB = PQ =2a, si on donne un mouvement circulaire uniforme à P : ,  le point Q a pour mouvement : . Le point M est défini par . Quartique bicirculaire rationnelle ayant un axe de symétrie (et on les obtient toutes ainsi).

 

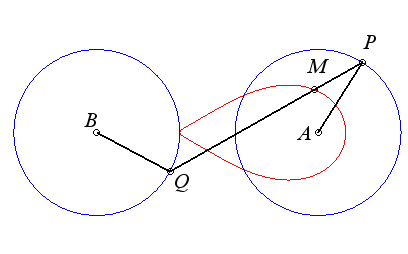
Une courbe de l'antiparallélogramme (ou du contre-parallélogramme) articulé est le lieu d'un point M de la bielle [PQ] d'un quadrilatère articulé (APQB) dont les côtés opposés sont de même longueur, A et B étant fixes - c'est donc une courbe du trois-barres à manivelles de même longueur dont la bielle a une longueur égale à la distance entre les pivots. C'est le seul cas où les bielles du mécanisme du trois-barres effectuent des rotations complètes (voir [Pécaud]). On ne regarde que le cas ou (APQB) est croisé, le cas du parallélogramme donnant de simples cercles. Lorsque le point M est au milieu de la bielle, on obtient les courbes de Booth.

 

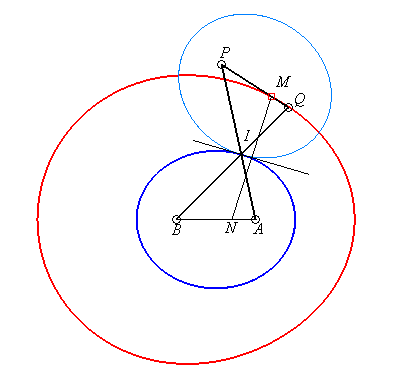
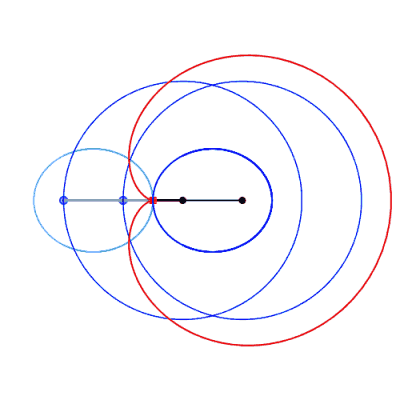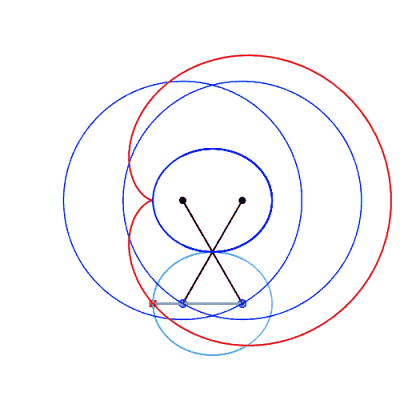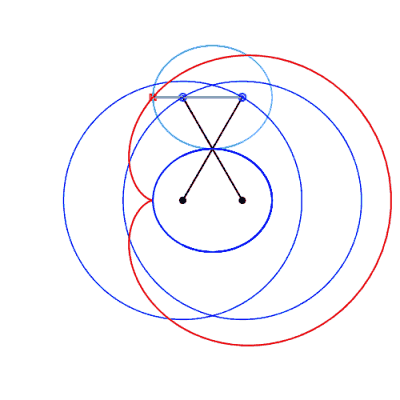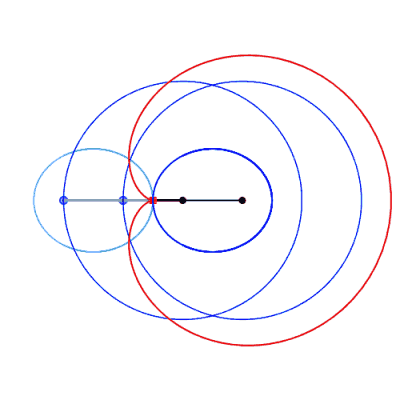
Cas où la bielle est plus courte que les manivelles (a < b). Les deux manivelles se croisent en un point I ; les triangles IAB et IPQ étant isométriques, on a 2IA + 2IB = IA + IQ + IB + IP =AP + BQ = 4b :  le point I décrit une ellipse de foyers A et B, de demi grand axe b et de demi petit axe . Le point M est le symétrique du point  par rapport à la tangente en I à l'ellipse qui est l'axe de symétrie de l'antiparallélogramme. La courbe décrite par M est donc l'orthotomique de l'ellipse par rapport au point N. L'ellipse symétrique, de foyers P et Q roule sans glisser sur l'ellipse fixe. Les courbes considérées ici sont donc les podaires d'ellipse par rapport à un point situé sur l'axe focal. Le point N est un point singulier de la courbe : il est isolé s'il est à l'intérieur de l'ellipse (cas de la figure ci-contre), point de rebroussement s'il est situé sur l'ellipse (courbe cuspidale), point de croisement s'il est extérieur à l'ellipse (courbe crunodale). Le cas isolé, où la courbe a une forme d'oeuf, se produit donc si . A droite, exemple d'un cas cuspidal : .
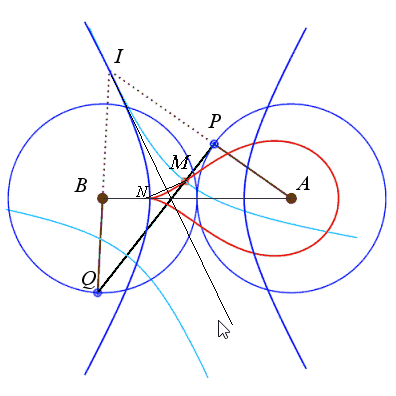
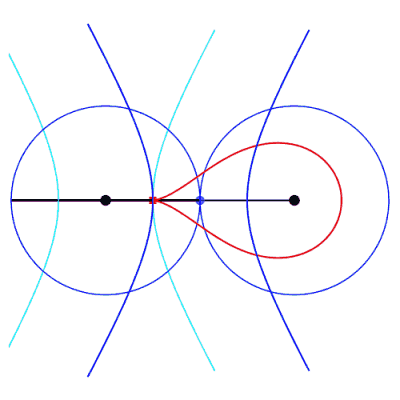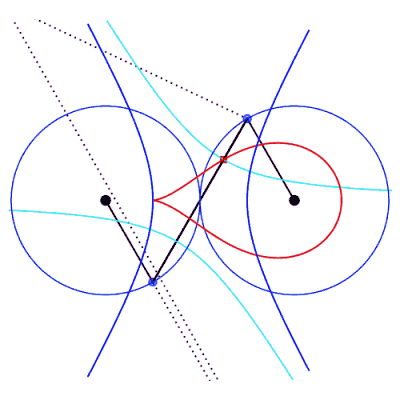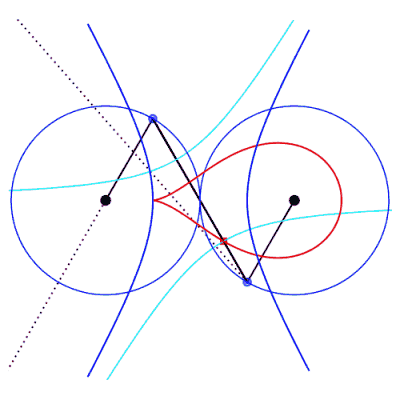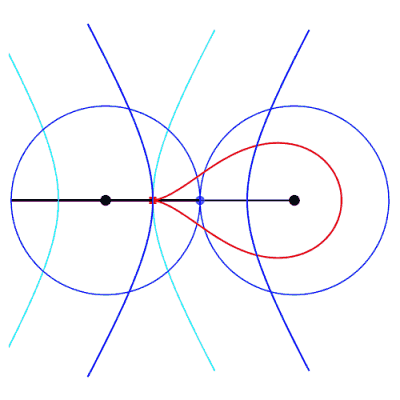
Cas où la bielle est plus longue que les manivelles (a > b). Les deux manivelles prolongées se croisent en un point I de l'axe de symétrie de l'antiparallélogramme et IP = IB par symétrie. Donc IA – IB = IP + PA – IB = AP  = 2b, et le point I décrit une hyperbole de foyers A et B, de demi axe focal b et de demi axe transverse . Le point M est le symétrique du point  par rapport à la tangente en I à l'hyperbole qui est l'axe de symétrie de l'antiparallélogramme. La courbe décrite par M est donc l'orthotomique de l'hyperbole par rapport au point N. L'hyperbole symétrique, de foyers P et Q roule sans glisser sur l'hyperbole fixe. Les courbes considérées ici sont donc les podaires d'hyperbole par rapport à un point situé sur l'axe focal. Le point N est un point singulier de la courbe : il est isolé s'il est à l'intérieur de l'ellipse, point de rebroussement s'il est situé sur l'ellipse (courbe cuspidale), point de croisement s'il est extérieur à l'ellipse (courbe crunodale). Le cas isolé se produit donc si . A droite, exemple d'un cas cuspidal : .

 

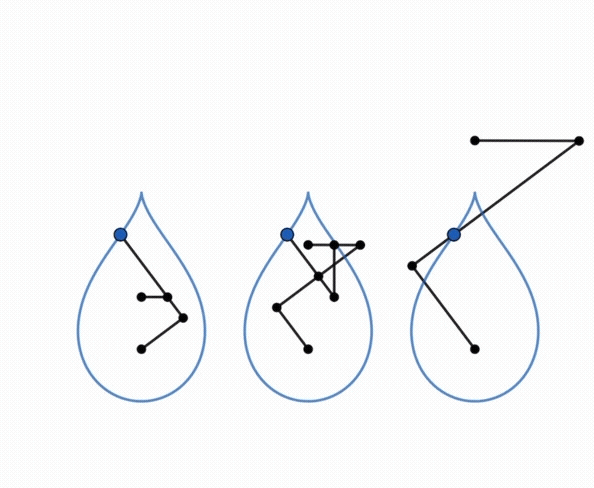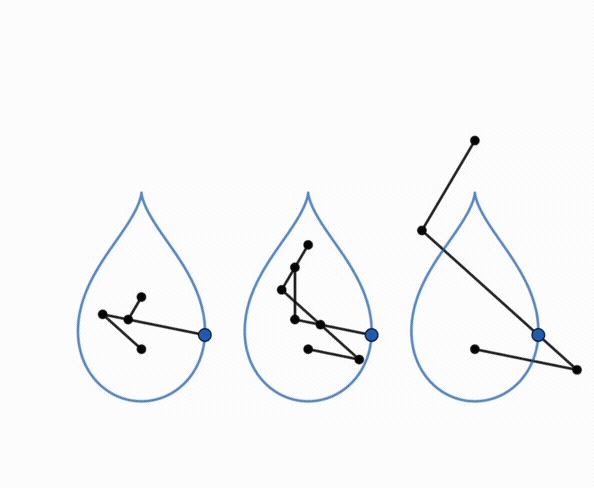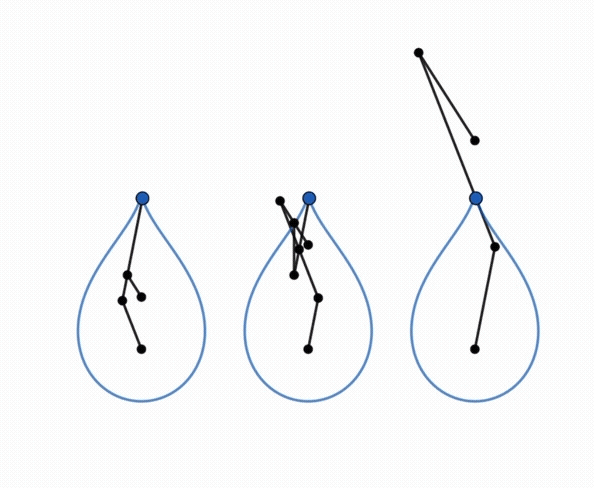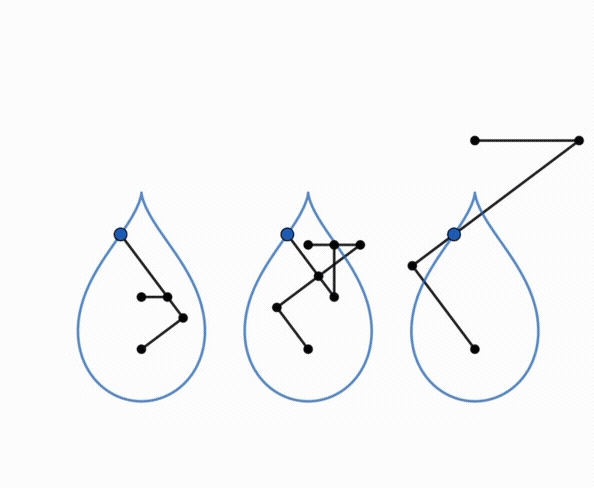
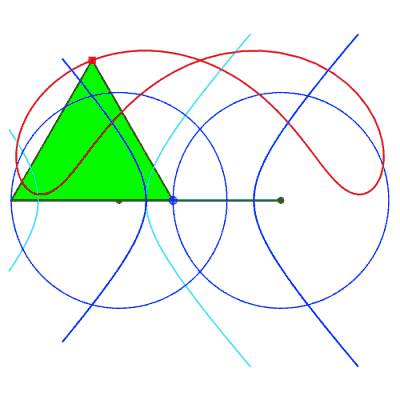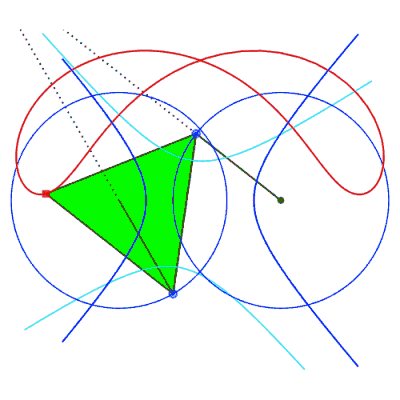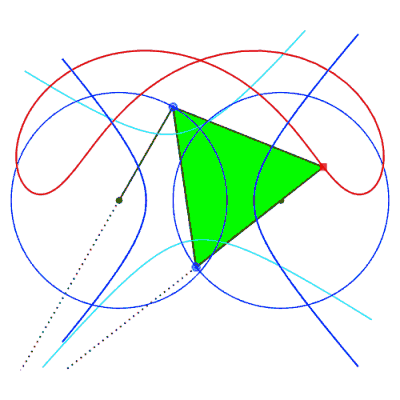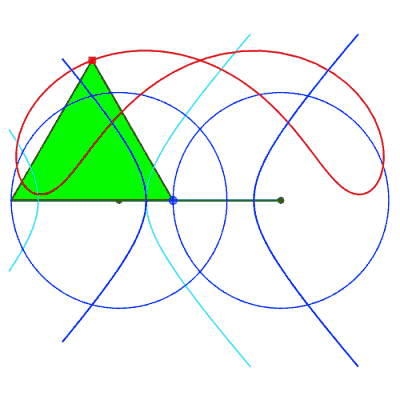
Comme toute courbe du trois-barres, ces courbes ont une triple génération par système articulé. Animation ci-contre dûe à Keishiro Ueki.
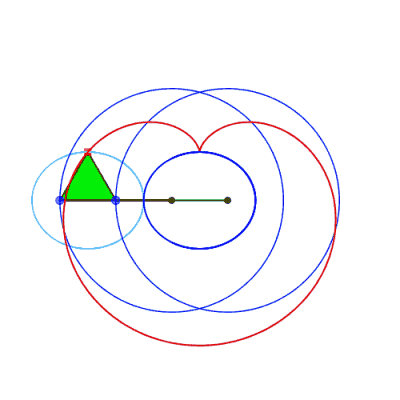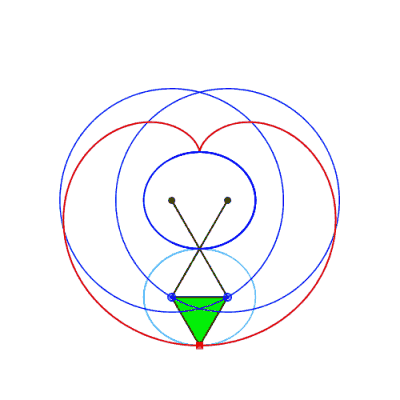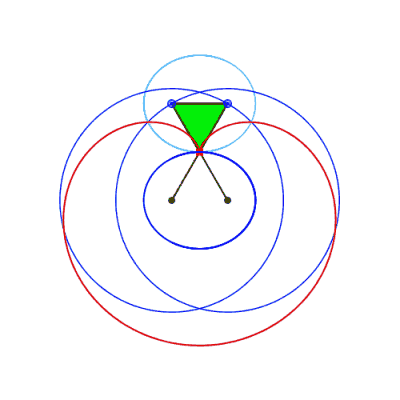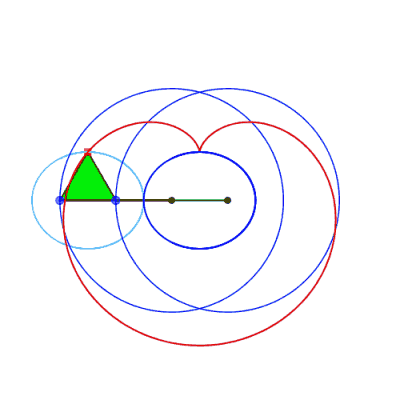
On peut généraliser à une roulette du plan associé à la bielle. On obtient ainsi toutes les quartiques bicirculaire rationnelles.

 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2023