courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

COURBE DU TROIS-BARRES
Three(or four)-bar linkage (or mechanism) curve, Kurve des drei-(or vier-)gliedrigen Koppelgetriebes


Les courbes tracées ici sont des 1/2 courbes du trois-barres


Courbe étudiée par Tchebicheff en 1868, Cayley et Roberts en 1875, Darboux en 1879 et Koenigs en 1897.
KOENIGS, leçons de cinématique, Hermann, 1897, p. 246 à 299 ; BROCARD LEMOYNE T 2 p 116 ;
BRICARD, cinématique et mécanismes, A. Colin , 1947 ; H. Lebesgue, Leçons sur les constructions géométriques, 1950 ;
ROSENAUER, WILLIS, kinematics of mechanisms, Dover, New York, 1967 ; HUNT, Kinematics, geometry of mechanisms, Oxford University Press, 1978 ; 
F. RIDEAU, les systèmes articulés, Pour La science n° 136, février 1989 ; Au dela du compas expos. du Palais de la Découverte p. 54 à 57.
F. PECAUT : les quadrilatères articulés
Voir aussi le site d'alain Esculier pour les explications sur les animations de cette page.

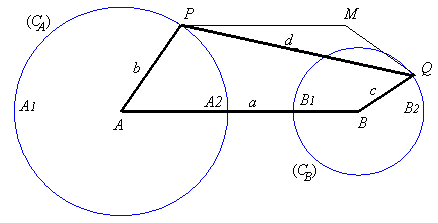
Une courbe du trois-barres est le lieu d’un point fixé M du plan lié à la barre [PQ] d'un quadrilatère articulé (APQB), A et B étant fixes. Les trois «barres» en question sont [AP] et [BQ] (appelés les manivelles ou les balanciers) - et [PQ] (appelé la bielle, ou le couple).
 
Nous choisissons A(0, 0), B(0, a), AP = b, BQ = c, PQ = d.

En prenant des lettres minuscules pour les affixes des points, on a :
, t et u étant reliés par la relation .
Équation cartésienne (Roberts) : 
où 
Sextique  tricirculaire, elliptique sauf quand , où la courbe est rationnelle.
Il y a trois points doubles (réels ou non) sur le cercle LP = MN.

Une courbe du trois-barres est donc le lieu d'un point lié à un segment de longueur constante joignant deux cercles - les cercles (CA) et (CB) de centres A et B et de rayon b et c.

Lorsque les manivelles ont même longueur et M est le milieu [PQ], on obtient une courbe de Watt.
Lorsque les manivelles ont même longueur et que la bielle a un longueur égale à la distance entre les pivots de base, on obtient un cercle ou une courbe de l'antiparallélogramme articulé.

La courbe est non vide si et seulement s'il existe au moins un quadrilatère de côtés de longueurs a, b, c et d, soit si chacun de ces quatre nombres est inférieur ou égal à la somme des autres, soit encore

On dit que le point P est à révolution complète s'il peut décrire le cercle (CA) entier (même définition pour Q) ; en mécanique le bras [AP] est appelé une manivelle quand il y a rotation complète, et un balancier sinon ; on démontre que si A1 est le point d'intersection de gauche de (CA) avec (AB), et A2 celui de droite, le point P passe par A1 ssi  et le point P passe par A2 ssi  . Le point P est à révolution complète ssi ces deux conditions sont réalisées et pour le point Q, il y a 2 inégalités similaires obtenues en échangeant b et c.

La courbe est formée d'une seule composante si et seulement pour P et Q l'une des 2 inégalités ci-dessus est réalisée (??).
 

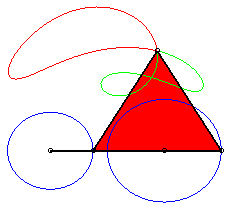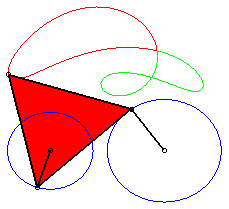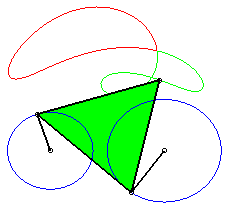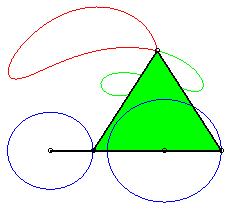
a = 4 ; b  =1,5 ; c = 2  ; d = a + c - b ;
Cas (limite) où P est à révolution complète ; Q traverse l'axe à droite mais ne fait pas une révolution complète.

a = 4 ; b  =2 ; c = 7 ; d = a  ;
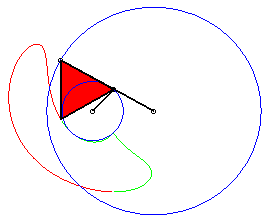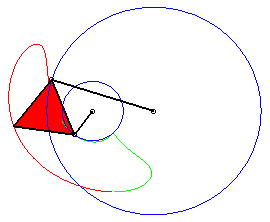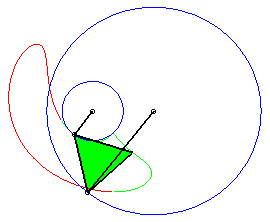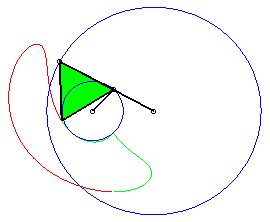
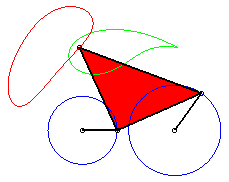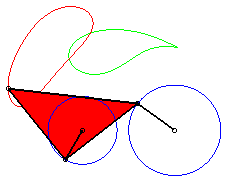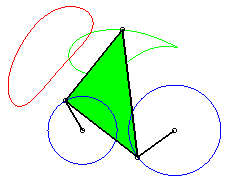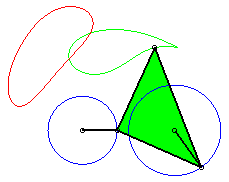Pas de point à révolution complète, mais P et Q traversent l'axe à gauche.
a = 4 ; b = 1,5 ; c = 2 : d = a 
P est à révolution complète, mais Q ne traverse pas l'axe : la courbe est formée de deux composantes (qui se chevauchent : elle est donc connexe !).

 
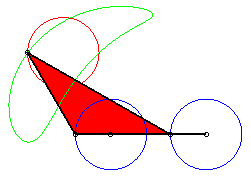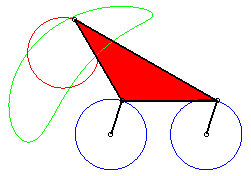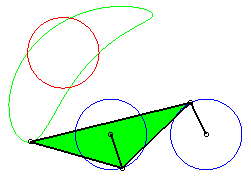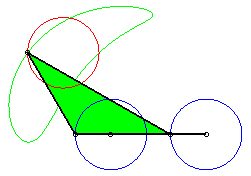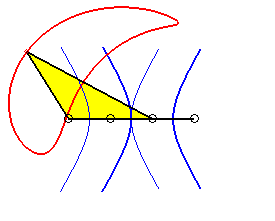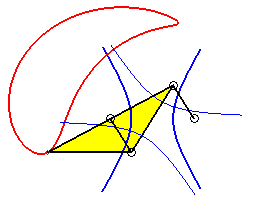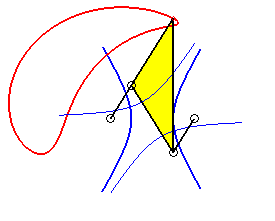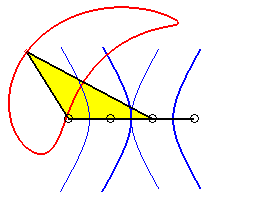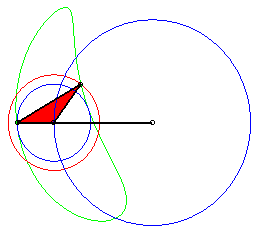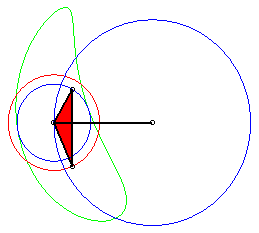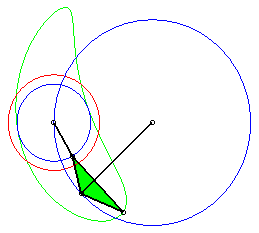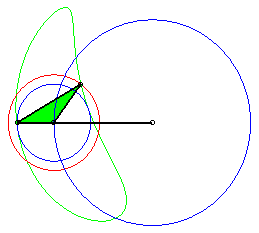
Cas du parallélogramme et du contre-parallélogramme (a = d et b = c) : seul cas où P et Q sont à révolution complète ; la courbe se décompose en un cercle et une quartique bicirculaire rationnelle, qui est une podaire d'ellipse quand a < b  ou d'hyperbole quand a > b (la bielle est l'axe focal d'une conique à centre roulant sur une conique égale).

Cas du rhomboïde (a = c et b = d)
D'après le principe de l'échange de bielle et manivelle (voir plus loin), la courbe obtenue est semblable à la précédente.

La courbe est générée de deux autres façons par deux autres trois-barres [BRSC] et [CTUA] (théorème de triple génération de Roberts) :
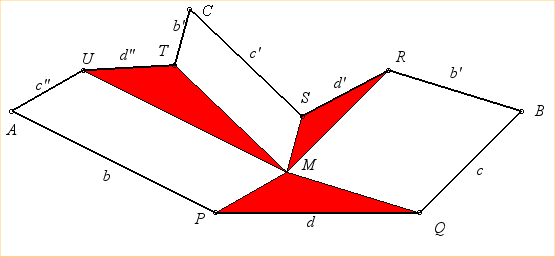Les trois quadrilatères blancs sont des parallélogrammes, et les trois triangles rouges sont semblables ; par conséquent :
r = b + m – q ; u = a + m –p ;
s = r + (m – q)(m – r)/(p – q) ;
t = m + (m – q)(m – u)/(q – p) ;
c = t + s – m.
(b', d', c') est proportionnel à (d, c, b) et
(b" ,d", c")  à (c, b, d).
Le triangle (ABC) reste fixe.

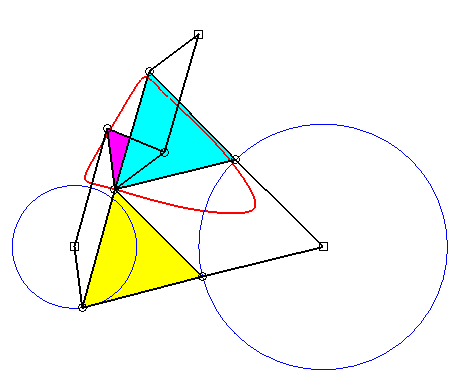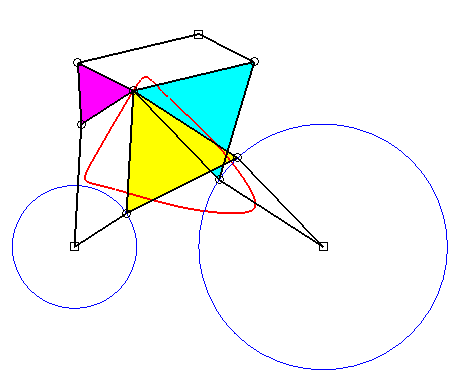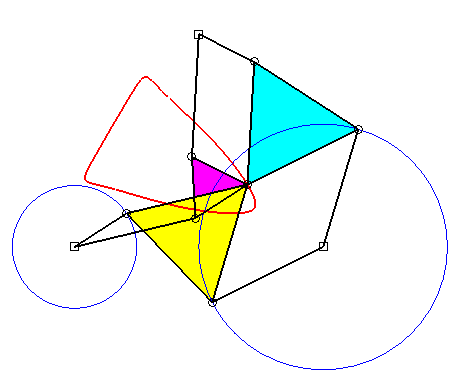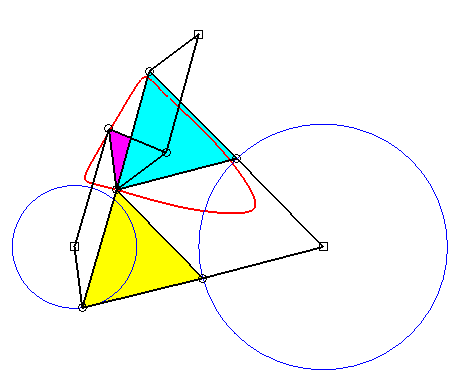Superbe animation de la triple génération de Roberts due à Alain Esculier.

On en déduit le principe de l'échange de bielle et manivelle, affirmant que si l'on échange la bielle avec une manivelle, les courbes décrites à l'aide du nouveau dispositif sont semblables à celles de départ.

Dans le cas b = c = d et triangle équilatéral (cas étudié par François Rideau) : le dispositif de triple génération présente une symétrie d'ordre 3, donc également la courbe ; si l'on pose k = 3b / a on obtient les formes suivantes :
 
k < 3/2  : triangle arrondi

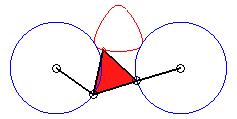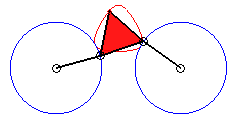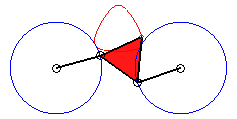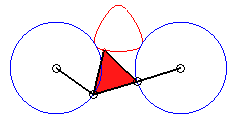
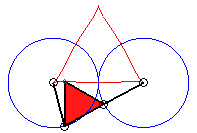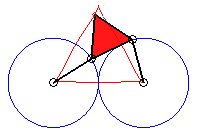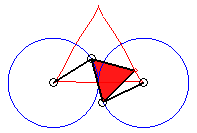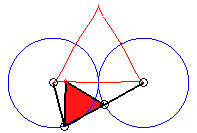
k = 3/2 : quasi triangle

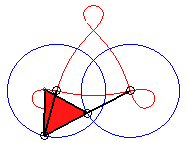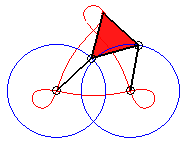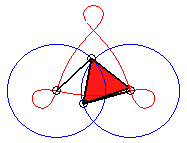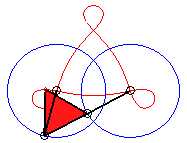
 3/2 < k < 3

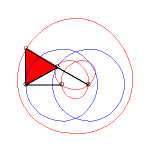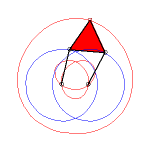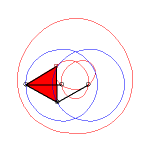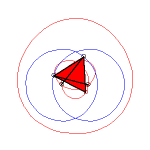
k > 3

Le cas a = 2d, b = c =QM = MP,  correspond au mécanisme de Roberts permettant d'obtenir une courbe quasi rectiligne (voir aussi à courbe de Watt).
 

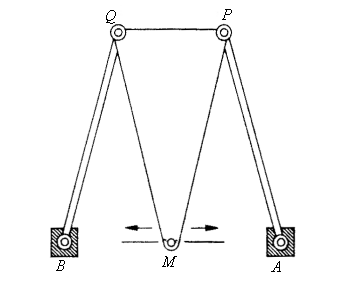
la courbe passe par A, B et le milieu de [AB]
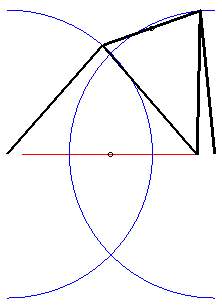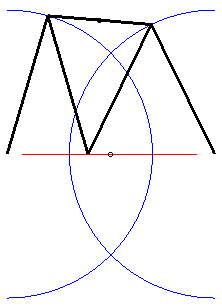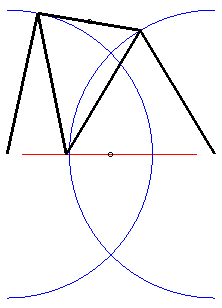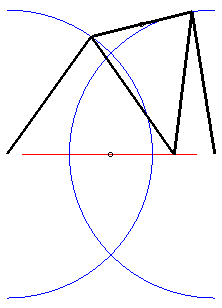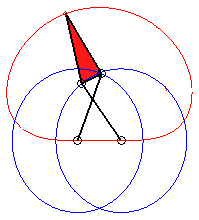la courbe complète (enfin, à compléter avec son symétrique par rapport à [AB]) n'a théoriquement aucune portion rectiligne.

Enveloppe de la bielle ?
 
 
Les courbes du trois-barre sont des cas particulier de glissettes, lorsque les courbes fixes et glissantes sont des cercles.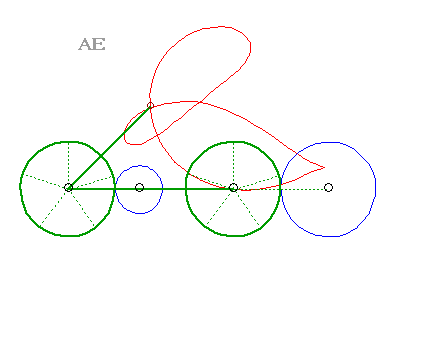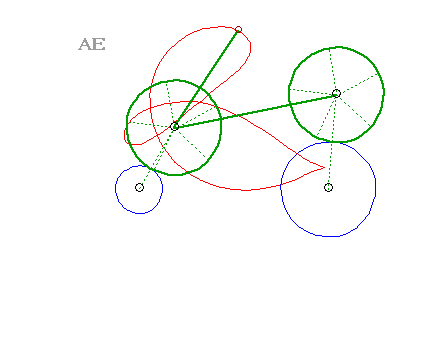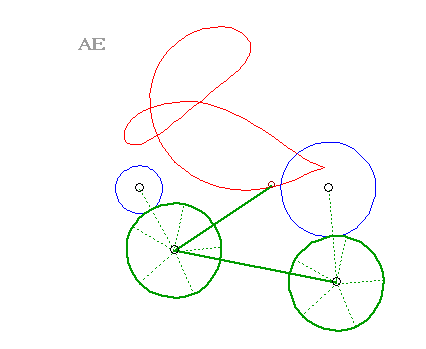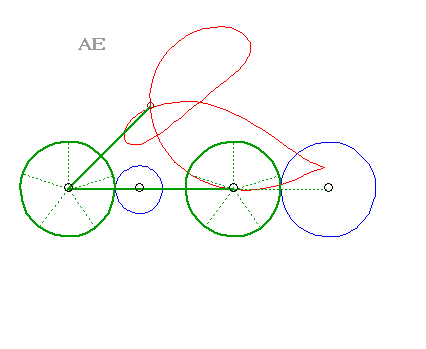

On a généralisé ces courbes au cas d'un segment de longueur fixée (toujours appelé la bielle) dont les extrémités sont astreints à se déplacer sur deux courbes données, ce qui est aussi un cas particulier de glissette.

Lorsque ces 2 courbes sont des droites non parallèles, les points liés à la bielle décrivent des ellipses, (théorème de La Hire), tandis que la bielle enveloppe une tétracuspide (?) ; ce mécanisme est à la base du trace-ellipse d'Archimède.

Lorsque l'une est une droite et l'autre un cercle, on obtient les courbes de la bielle de Bérard et plus généralement lorsque l'une est une droite et l'autre une conique, on obtient les courbes polyzomales.

Site à visiter absolument :php.math.unifi.it/archimede/archimede/curve/geomeccan0.php?id=8

Voir aussi le L-système à trois barres. et la courbe du quatre-barres.
 
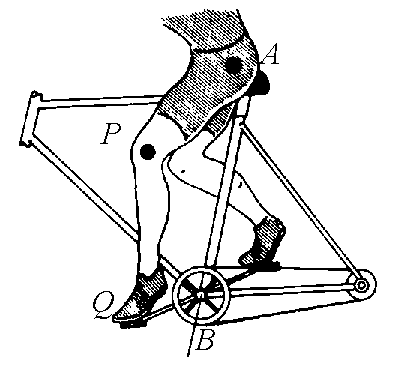
Les points de la jambe du cycliste décrivent (dans le repère lié au vélo), des courbes du trois-barres. Les points de sa cuisse décrivent de simples arcs de cercle ! Les pieds de ce sportif décrivent des courbes du trois-barres. La machine s'appelle un vélo elliptique, mais où sont diable les ellipses ?

 
 
courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL, Alain ESCULIER 2016