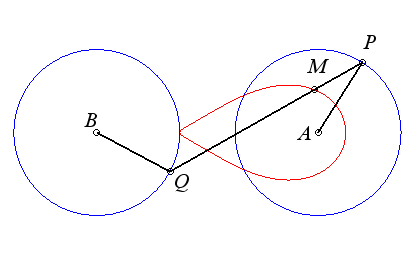
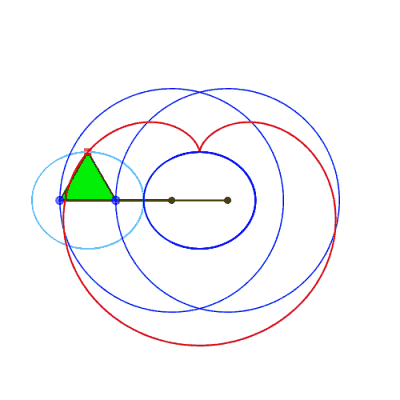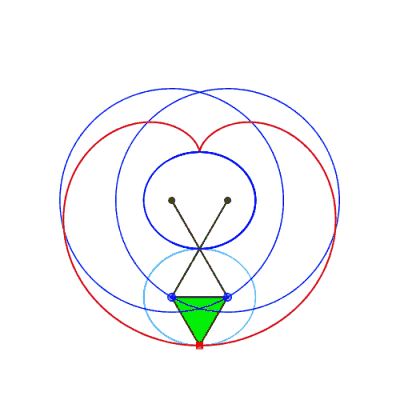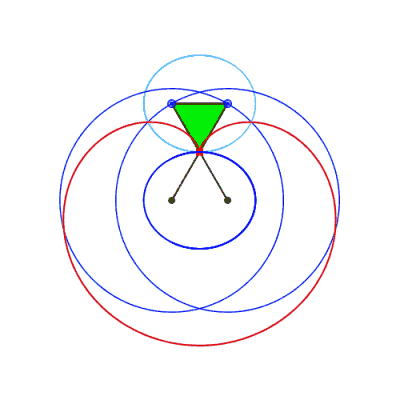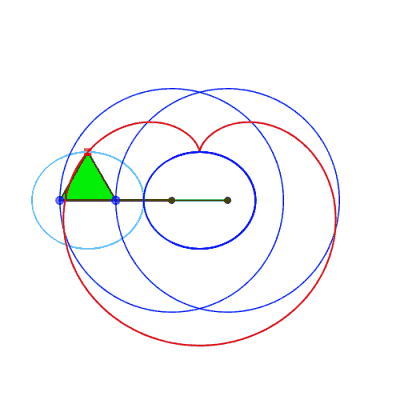
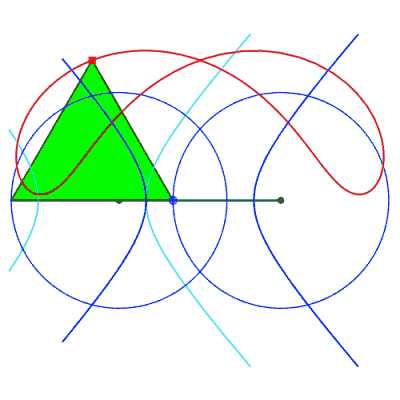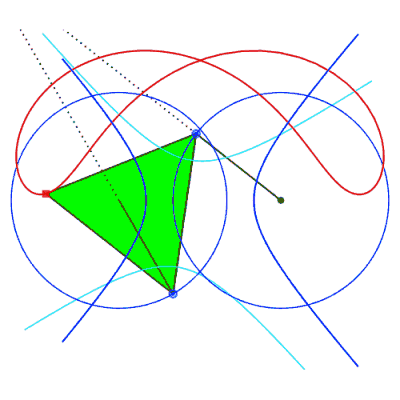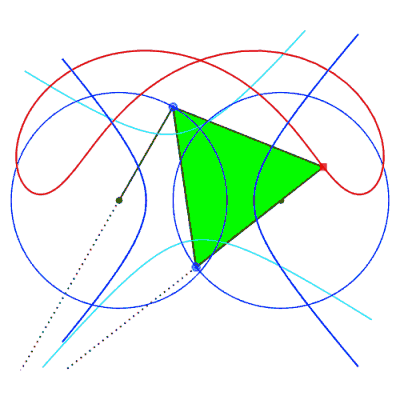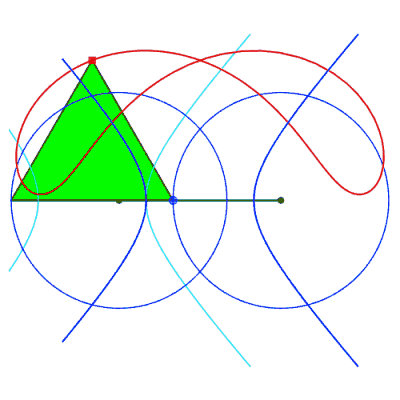
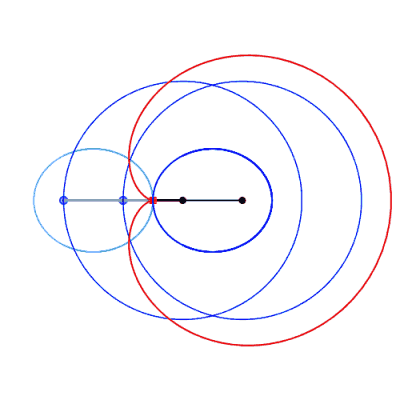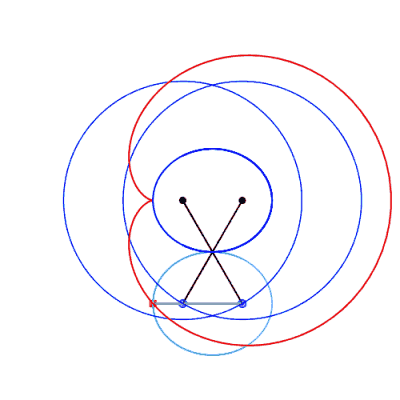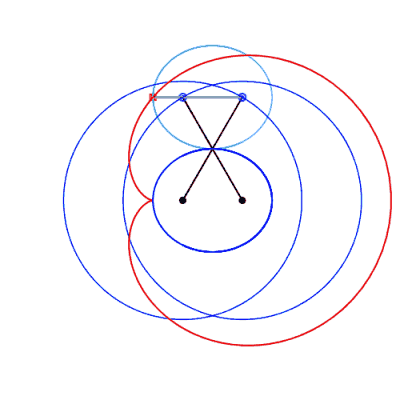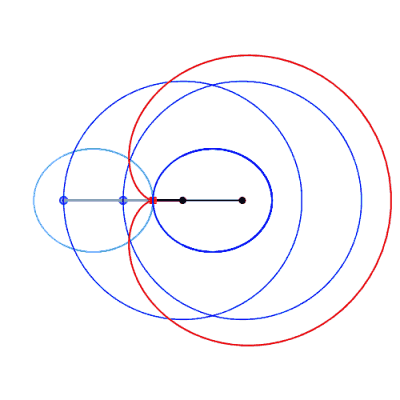
Case where the connecting rod is shorter than the cranks
(a < b).
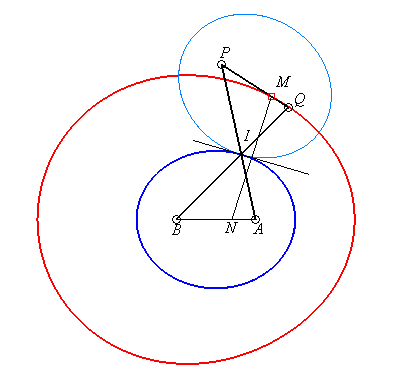
The two cranks intersect at a point I; the triangles
IAB and IPQ being congruent, we have 2IA + 2IB
= IA + IQ + IB + IP =AP + BQ = 4b:
the point I describes an ellipse with foci A
and B, semi-major axis b and semi-minor axis 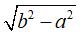 . .
The point M is the mirror image of the point with
respect to the tangent in I to the ellipse which is the axis of
symmetry of the antiparallelogram.
The curve described by M is therefore the orthotomic
curve of the ellipse with respect to the point N.
The symmetrical ellipse, with foci P and Q,
rolls without slipping on the fixed ellipse.
The curves considered here are therefore the pedal
curves of an ellipse with respect to a point located on the focal axis.
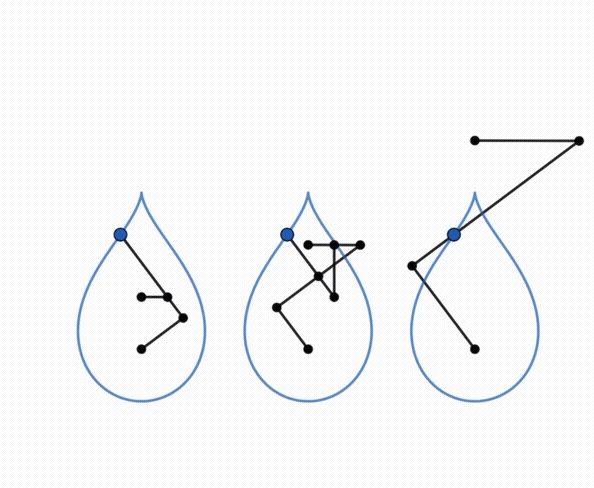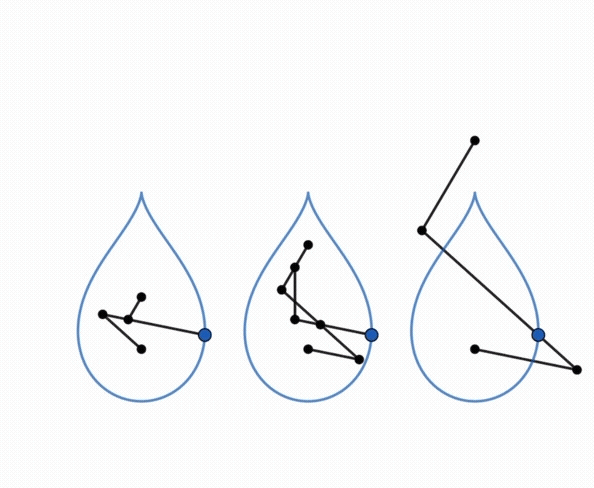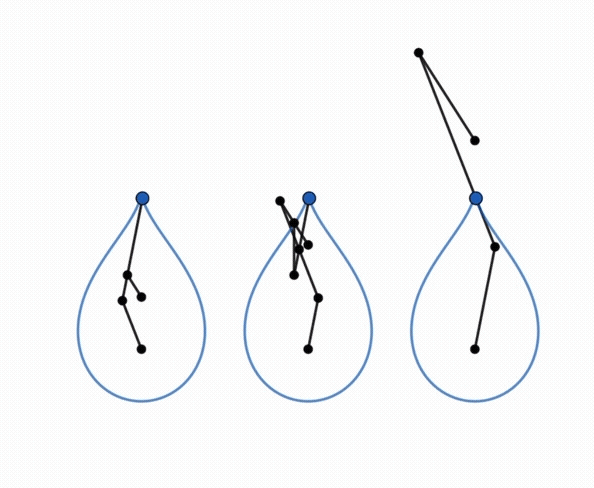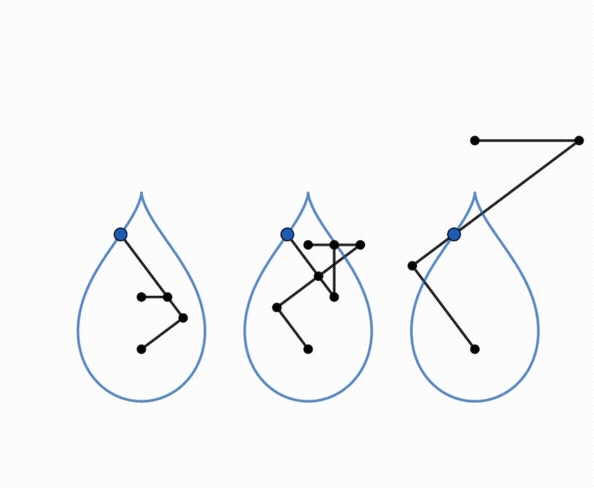
The point N is a singular point of the curve:
it is isolated if it is inside the ellipse (case of the figure opposite),
a cusp point if it is located on the ellipse (cuspidal curve), a crossing
point if it is exterior to the ellipse (crunodal curve).
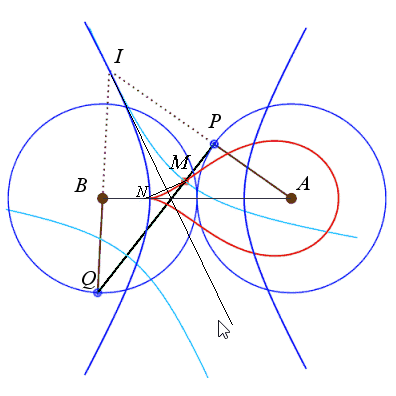
The isolated case, where the curve has an egg shape,
therefore occurs if 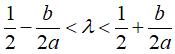 . .
Right, example of a cuspidal case: 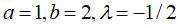 . . |
 |
|
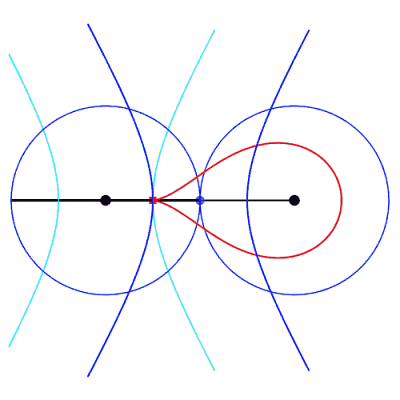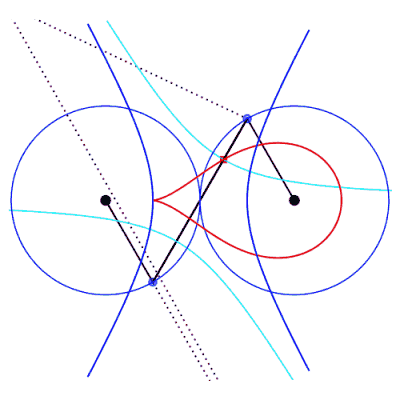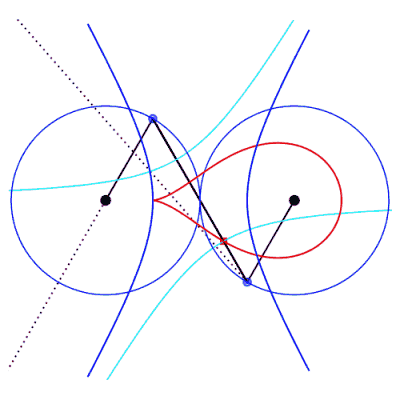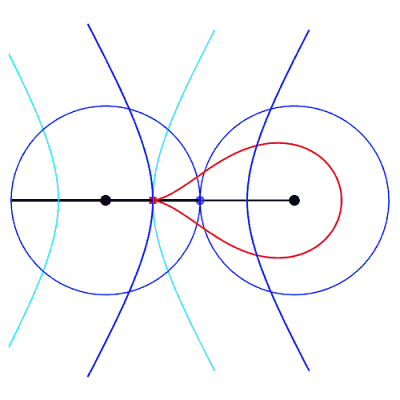
Case where the connecting rod is longer than the cranks (a
> b).
The two extended cranks intersect at a point I
of the axis of symmetry of the antiparallelogram and IP = IB by
symmetry. So IA – IB = IP + PA – IB = AP = 2b, and point
I describes a hyperbola with foci A and B, with focal
half-axis b and transverse half-axis 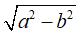 . .
The point M is the mirror image of the point 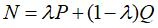 with respect to the tangent in I to the hyperbola which is the axis
of symmetry of the antiparallelogram.
with respect to the tangent in I to the hyperbola which is the axis
of symmetry of the antiparallelogram.
The curve described by M is therefore the orthotomic
curve of the hyperbola with respect to the point N.
The symmetrical hyperbola, with foci P and Q,
rolls without slipping on the fixed hyperbola.
The curves considered here are therefore pedal
curves of hyperbola with respect to a point located on the focal axis.
The point N is a singular point of the curve: it is isolated if
it is inside the ellipse, a cusp point if it is located on the ellipse
(cuspidal curve), crossing point if it is outside the ellipse (crunodal
curve).
The isolated case therefore occurs if 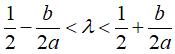 . .
Right, example of a cuspidal case: 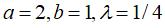 . . |
 |
|
,
.
.