| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
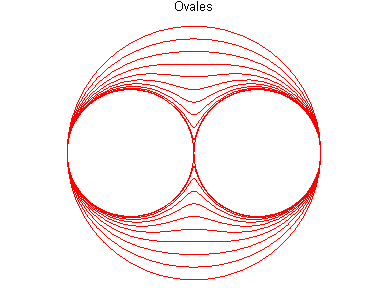
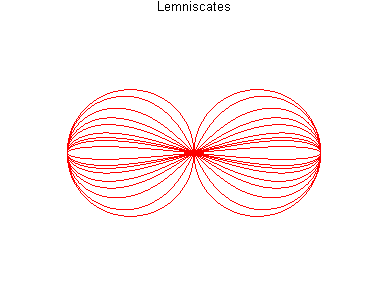
BOOTH'S CURVE, OVAL, LEMNISCATE
|
|
|
| Curves studied by Fagnano in 1750, Euler in 1751, and
Booth in 1877.
James Booth (1810 -1878): British mathematician. Other names: Hippopede of Proclus, elliptic lemniscate (for the ovals) and hyperbolic lemniscate (for the lemniscates). |
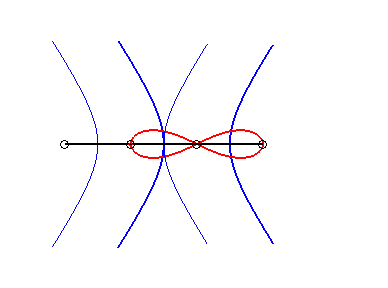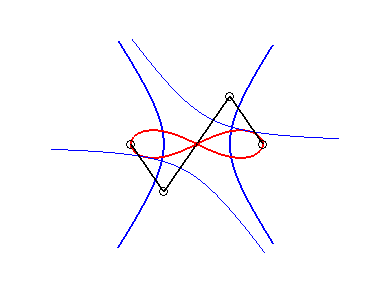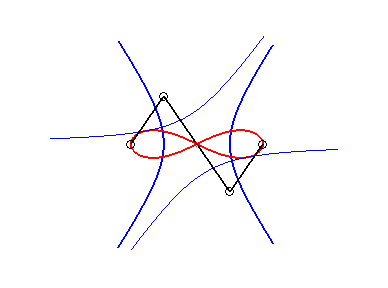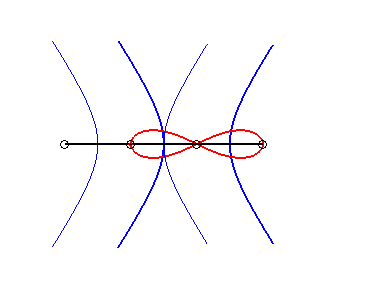
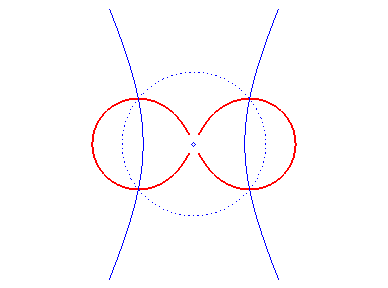
Cartesian equation: 
;
with e = 1 for the ovals (take 0 <  ),
e
=
–1 for the lemniscates.
Polar equation: Tripolar equation: with |
Booth's curves are the rational bicircular quartics possessing point symmetry.
As do all rational bicircular quartics, they have four equivalent definitions:
1) They are the pedals
of centred conics with respect to their centre (here, pedal with respect
to O, of the conic 
).
- For an ellipse, Booth's curve is
called Booth's oval; they are true ovals (i.e. convex) only for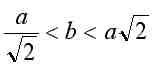 
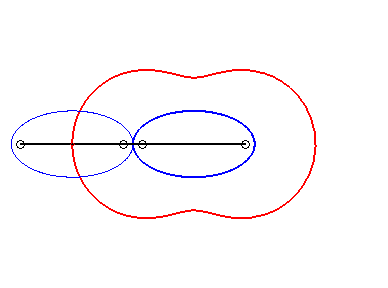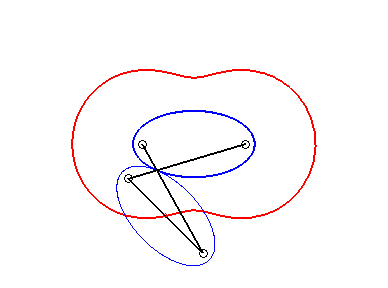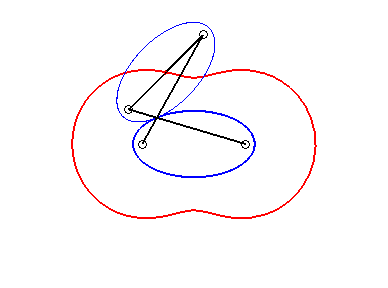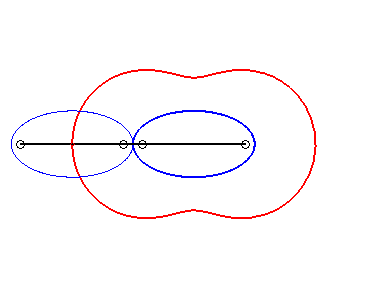
(and it is a circle for a = b); it is shaped
like a bean in other cases.
 |
From this we deduce that an oval of Booth is the locus of the centre of an ellipse rolling without sliding on an equal ellipse, with coinciding vertices, it is therefore also a curve of the three-bar mechanism (see further on the interpretation as a curve of Watt) |
- For a hyperbola, it is called Booth's
lemniscate
because of its 8-like shape. We get a lemniscate
of Bernoulli when the hyperbola is rectangular.
 |
 |
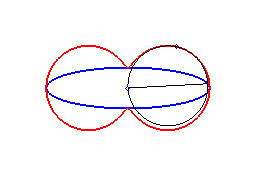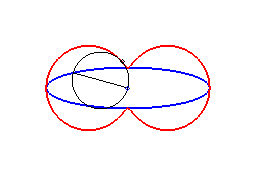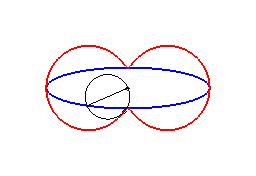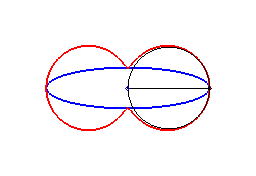
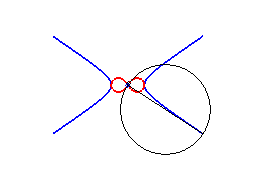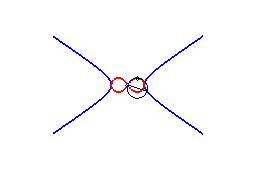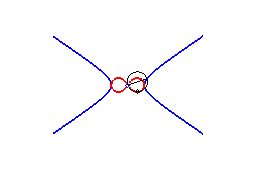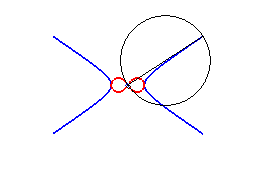
2) They are the envelopes of the circles whose diameters join the centre of a conic to any point on this conic.
3) They are the inverses
of centred conics with respect to their centre (here, of the conic 
if ab is the radius of inversion - note the permutation of a
and b with respect to 1) ).
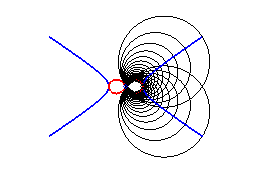
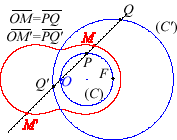
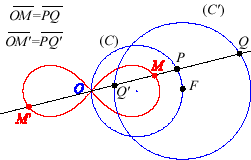
4) They are the cissoidal
curves of two circles (C) and (C') with respect to a
point O such that O belongs to (C) and the centre
of (C') is the point F on (C) diametrically opposed
to O. The point F is any of the focal points of the conic
from 1) ; here for example F
, a being the radius of (C').
 |
 |
But they also have 4 different remarkable definitions:
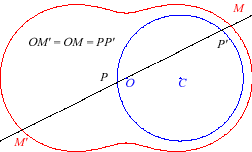
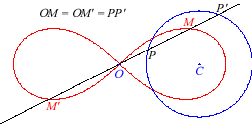
5) They are the cissoidal
curves of two coinciding circles with respect to any point. We get
an oval or a lemniscate depending on whether the point in inside or outside
the circle. We get the lemniscate
of Bernoulli when the point is at distance
times the radius of the circle.
Here the circle is the circle of centre 
(middle of [OF]) and radius a/2.
|
|
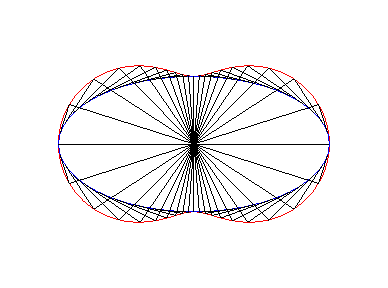
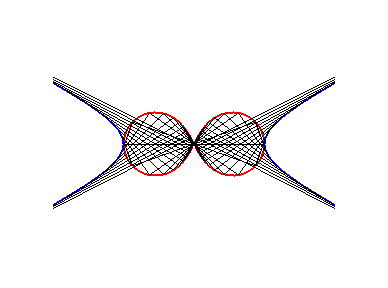
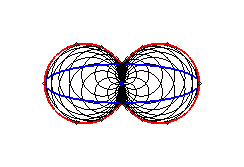
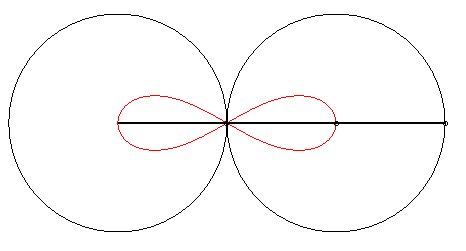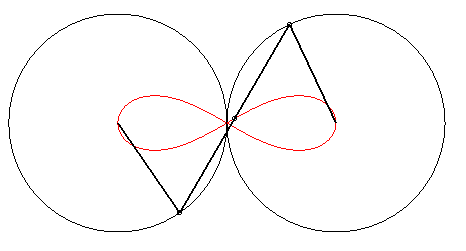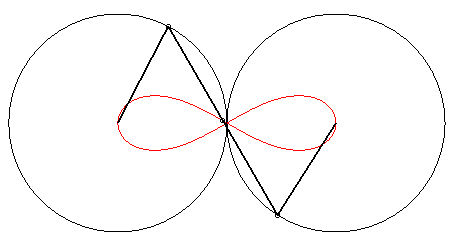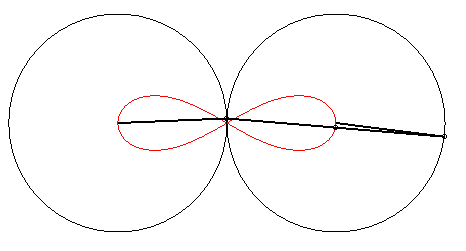
6) They are examples of Watt's
curves; they are the loci of the middle of a segment line of length
2d joining two circles of radius a the centres of which are
at distance 2d. In other words, they are the loci of the middle
of a side (of length 2d) of an articulated "rectangle", the other
side (of length a) being fixed; we get lemniscates of the large
side is fixed, and ovals in the other case.
 |
 |
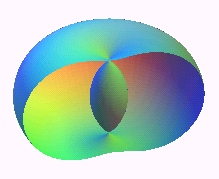
7) They are Perseus' spiric curves (i.e. sections of a torus by a plane parallel to its axis) when the plane is tangent to the interior of the torus. This definition is the reason for the name hippopede of Proclus. More precisely, they are the sections of a torus of centre O, axis Oz, major and minor radiuses a and b, cut by the plane parallel to Oz and at distance d =|a – b| of O. The curve is an oval when the torus is a spindle torus (b > a) and a lemniscate when it is a ring torus (a < b).
In a frame with the projection of O on the plane as the origin, we get the Cartesian equation:
.
 |
 |
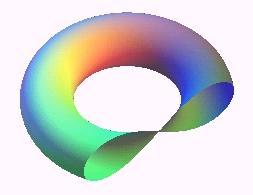8) They are the projections on xOy of the biquadratics
who are intersections of the paraboloid of revolution 
and the second degree cone 
.
9) If we apply the scaling in one direction 
to the oval 
,we
get a curve with polar equation 
where 
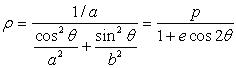
and 
;
therefore Booth's ovals are, up to scaling in one direction, polygasteroids.
Compare Booth's curves to Cassini's ovals.
See also Fresnel's
elasticity surface which is the generalisation to a 3D space of Booth's
oval.
See also Booth's lemniscate on the Roman
surface.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
.
in the reference triangle (F, F',O) where F(d,0)
and F'(–d,0),
,
.
( 
, 
)
(
for the ovals, 
for the lemniscates. 
