LEMNISCATE OF BERNOULLI

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
LEMNISCATE OF BERNOULLI

| Curve studied by Jacques Bernoulli in 1694 and Fagnano
in 1750.
Jacques Bernoulli (1654 -1705): Swiss mathematician. Other name : Bernoullian lemniscate. |
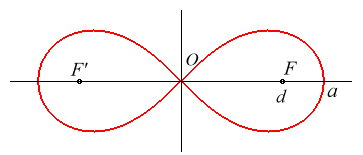 |
Bipolar equation: Tripolar equation: Polar equation: |
| Cartesian equation: Rational bicircular quartic. Cartesian parametrization: Rational Cartesian parametrization: hence the complex parametrization: Another Cartesian parametrization: Cartesian parametrization of the complexified curve: Complex equation: Pedal equation: Polar tangential angle: Curvilinear abscissa: Radius of curvature: Intrinsic equation: Length: We also have: |
The lemniscate of Bernoulli is a challenger, along with the cardioid, for the record number of memberships to various families of remarkable curves.
It is indeed:
| - a special case of Cassinian oval (see the bipolar equation) | |
| - a special case of Booth curve. | |
| - a special case of sinusoidal spiral (see the polar equation) | |
| - as all rational bicircular quartic, at the same time, the pedal with respect to O and the inverse (reference circle with diameter [A(a,0) ; A'(-a,0)]) of the rectangular hyperbola with centre O and vertices A and A'; F and F' are the inverses of the foci of this hyperbola and the tangents at the origin are the inverses of the asymptotes. | 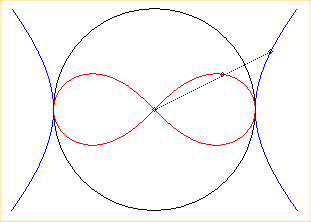 |
| - it is also, as a pedal curve, the envelope of the circles with diameters the ends of which are the centre and a point of this hyperbola. | |
| - as well as the locus of the centre of a hyperbola rolling without slipping on an equal hyperbola, with coinciding vertices. |
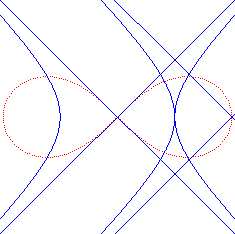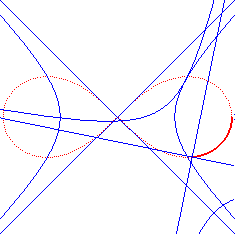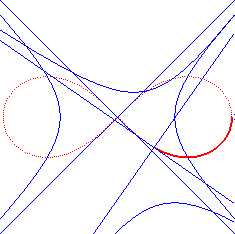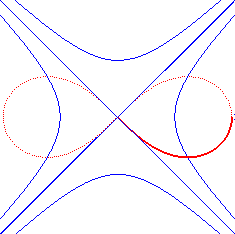 |
| - the cissoid
of the circle with centre F passing by O and the circle with
centre |
|
| - the cissoid with pole O of the circles (C)
and (C') with centres F and F' and radii
a/2.
In dotted lines, the circles (C) and (C'), in blue their homothetic image, the median of which is the lemniscate. |
 |
| - the locus of the middles of segment lines of length 2d the ends of which describe two circles with radius a centred on F and F'. |
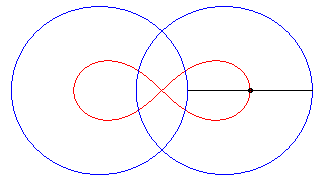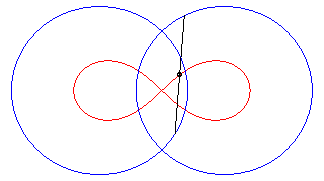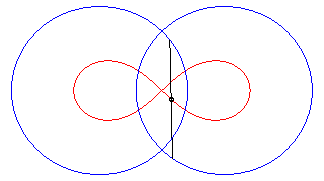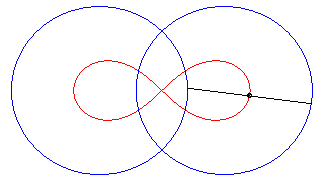 |
| Therefore, the lemniscate is a curve of the three-bar, in the special case of the Watt curve; according to the principle of the slider-crank exchange, there exists a second construction with an articulated quadrilateral: |
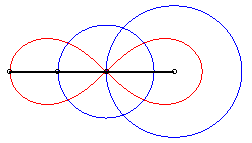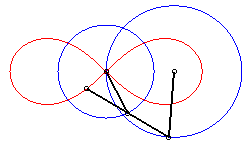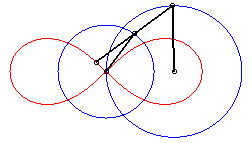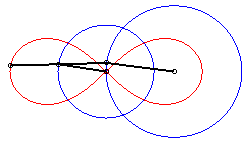 |
| - The section of a torus, with revolution radius d and meridian radius d/2, by a plane located at distance d/2 from the axis (the lemniscate is therefore a spiric of Perseus) |
 |
| - the curve passing by O the curvature of which is proportional to the distance to O (compare to the elastic curve, the curvature of which is proportional to the distance to a fixed line) | |
| - the locus of the points M such that |
|
| - the projection on the plane xOy of the
biquadratic: |
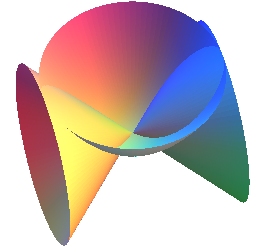 |
Furthermore:
- the asymptotic curves of the Plücker conoid are projected on lemniscates of Bernoulli.
- the lemniscate of Bernoulli is a synodal curve of all the intersecting lines passing by the double point:
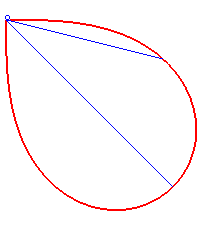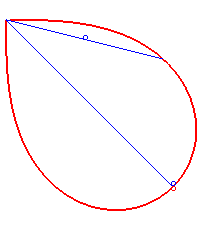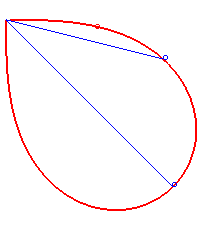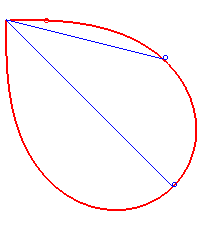
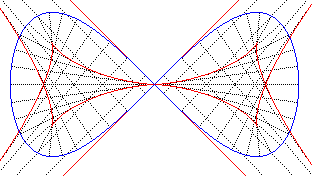
| The evolute
of the lemniscate of Bernoulli is parametrized by Notice that the two vertices correspond to maxima of the curvature... |
 |
| ...as opposed to the lemniscate of Gerono, where they correspond to minima... |
 |
| Generalisation: the pedal of the rectangular hyperbola
with respect to a point on the symmetry axis is a distorted lemniscate,
parametrized by |
 |

Watt mechanism to construct the lemniscate |
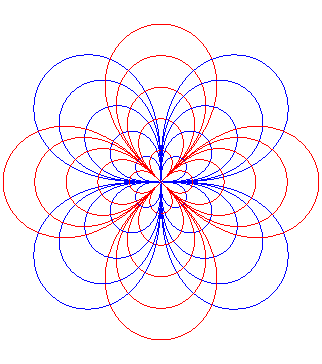
|
See here how
to "thicken" a lemniscate: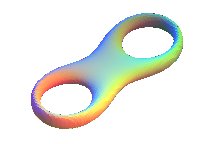 .
.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017