On désigne par tore à n trous, ou n-uple tore, ou sphère à n anses, tout espace topologique homéomorphe à la somme connexe du tore simple n fois par lui-même :  ; on pose par convention .
Caractérisation : surface connexe compacte sans bord orientable de genren.
La caractéristique d'Euler-Poincaré du tore à n trous vaut 2 – 2n.
 

Le double tore est familièrement appelé "bretzel". A droite, un bretzel mathématique formé de deux boucles de courbe de Viviani et d'un arc de cercle.

 

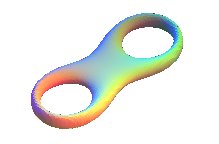
Un bretzel algébrique,de degré 4, à 2 plans de symétrie, d'équation ; cette équation a été bricolée à partir de celle du huit : , de façon à l'épaissir.
Partant de la lemniscate de Bernoulli, on obtient la figure du dessous, d'équation : .
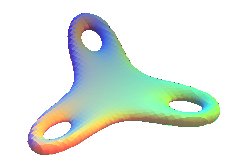
Un triple tore algébrique, construit à partir du trifolium régulier, d'équation : .
Un quadruple tore algébrique, d'équation : .

 

Le tore à n trous est aussi familièrement appelé "fougasse" : ci-contre, une fougasse à 6 trous.
Le rulpidon d'Ulysse Lacoste est un solide possédant quatre orifices, dont la surface est cependant homéomorphe au tore à trois trous (élargir l'un des orifices ; les trois autres forment les trous). Animation par Alain Esculier

Ne pas confondre le tore à n trous  avec le tore de dimension n,; en particulier, .

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2024