Reciprocal spiral

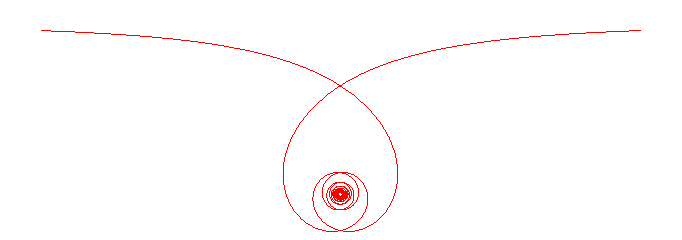
RECIPROCAL SPIRAL

Curve studied by P. Nicolas in 1696, Varignon in 1704, Bernoulli in 1710 and Cotes in 1722.

Polar equation:

.
Curvilinear abscissa:

.
Radius of curvature:

.
Transcendental curve.

The reciprocal spiral is the locus of the point M of a variable circle centred on O cutting the axis Ox at A such that the length of the arc AM is a constant equal to a.

Like the logarithmic spiral, it has a spiralling branch with an asymptotic point, but, contrary to the logarithmic spiral, its length is infinite.

Necessary and sufficient condition: curve for which the polar sub-tangent is constant.

It can also be obtained as
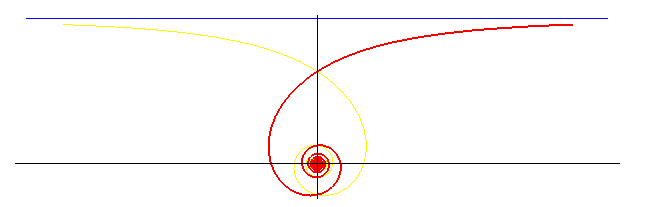
- the inverse of the Archimedean spiral
- the orthocaustic of the tractrix spiral with respect to the centre.
- the plane conical projection (the centre of the projection being on the axis and the plane of projection being perpendicular to this axis) of a circular helix (theorem of Théodore Olivier).

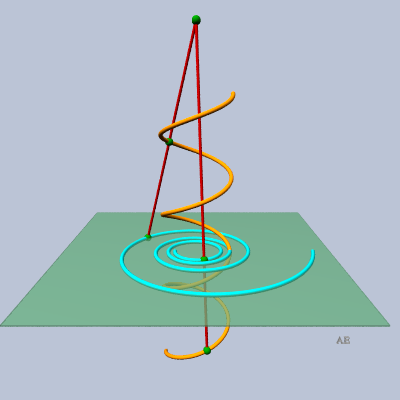It is the reason why the plunging view of a snail stairway is a reciprocal spiral.
See also this webpage of Gerard Lavau.
Le phare de la baleine à l'île de Ré

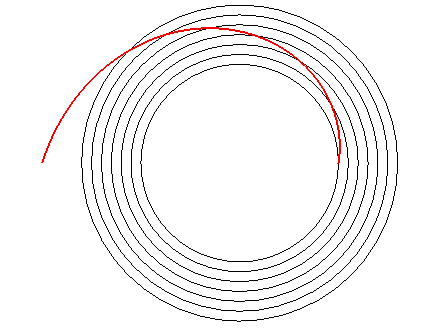
The curve providing the starting points of runners on a circular stadium is a reciprocal spiral:

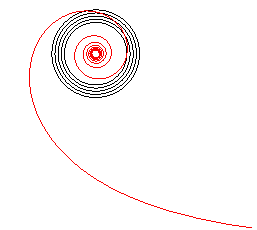If the radius of the internal circle is r, the equation of the reciprocal spiral is .

When a reciprocal spiral rolls on a line, its pole describes a tractrix, whereas when it rolls on a logarithmic curve, its pole describes a line.

The reciprocal spiral is the solution to the problem that consists in determining the trajectory in space of a massive point subject to a force centred on O and proportional to (this force is, according to the Binet formula, proportional to which, here, is equal to , with ); the other solutions are the epispirals and the Poinsot spirals, see this link.

See also the hyperbolic conical spiral, and compare to the SiCi spiral.

Doesn't the reciprocal spiral remind of the tail of a chameleon?

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra