Paramétrisation cartésienne :  n > 0. Équation cylindrique :  ; dans la suite, on fait a = b. Abscisse curviligne : . Rayon de courbure : , rayon de torsion : .

Les couronnes sinusoïdales sont les enroulements d'une sinusoïde autour d'un cylindre (autrement dit, si l'on fait rouler une couronne sinusoïdale sur un plan, on obtient une sinusoïde).

Ce sont des cas particulier de courbes de Lissajous 3D.
Les projections sur les plans contenant Oz sont les courbes planes de Lissajous, de paramètre n si n > 1 , 1/n sinon.

Pour n = 1 on obtient une ellipse, pour n = 1/2, la courbe de Viviani et pour n = 2, la courbe de la crêpe.

Pour n naturel, le nombre d'arches est égal à n. La couronne à trois arches est utilisée pour représenter les anneaux de Borromée.
 

Par projection horizontale sur la sphère de centre O et de rayon a, la couronne sinusoïdale devient la clélie : .

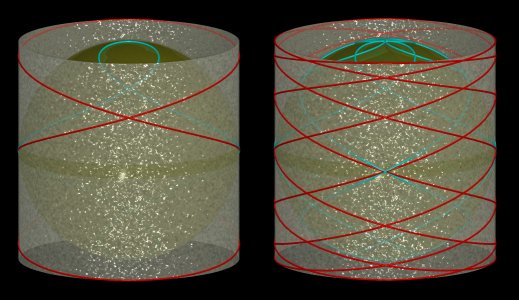
Figure réalisée par Alain Esculier

Voir aussi les sinusoïdes sphériques, les vasques 3D, les couronnes tangentoïdales et les tores sinusoïdaux.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2011