Courbe étudiée pour la première fois par Roberval en 1636, sous le nom de "compagne de la roulette". Le nom "compagne de la roulette" a été utilisé jusque vers 1850, conjointement à "courbe des sinus", puis devenu sinussoïde ou sinusoïde, ce dernier ayant pris le dessus.

 

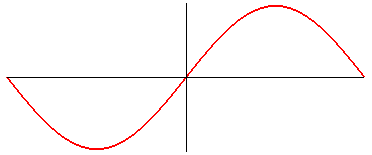Équation cartésienne : . Courbe transcendante. Longueur sur une période, donnée par une intégrale elliptique de deuxième espèce : . Dans le cas a = b : .

La sinusoïde est la trajectoire d'un mouvement composé d'un mouvement sinusoïdal (c'est-à-dire le projeté sur une droite d'un mouvement circulaire uniforme) et d'un mouvement de translation uniforme :

Si l'on enroule le plan de la sinusoïde en un cylindre de révolution de génératrice Oy et de rayon nb, on obtient la couronne sinusoïdale : .
Lorsque n  = 1, cette couronne est une ellipse d'excentricité , et donc, inversement, le développement d'une section plane d'un cylindre de révolution est une sinusoïde : concrètement, la trace du bord d'une bougie coupée en biseau, roulant sur un plan, est une sinusoïde :

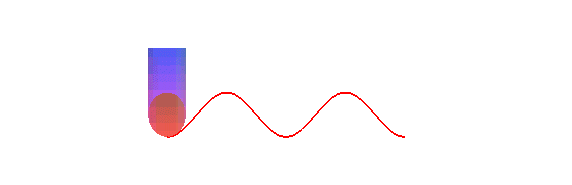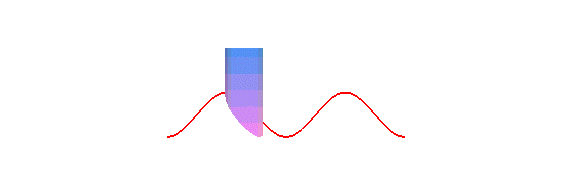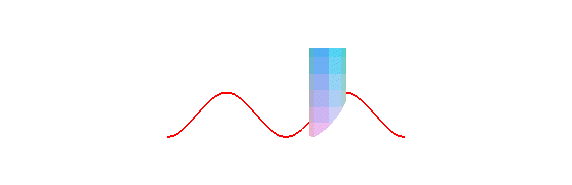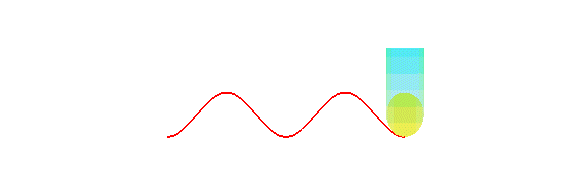
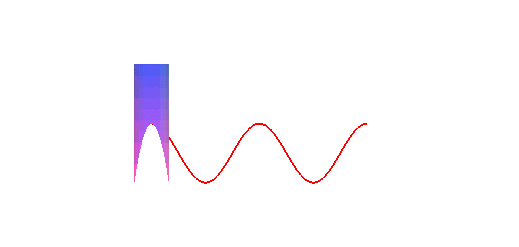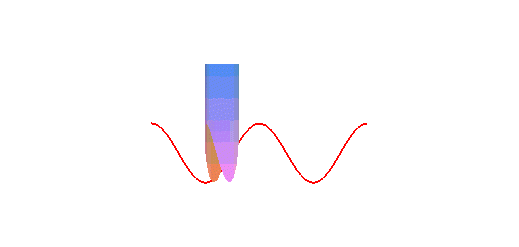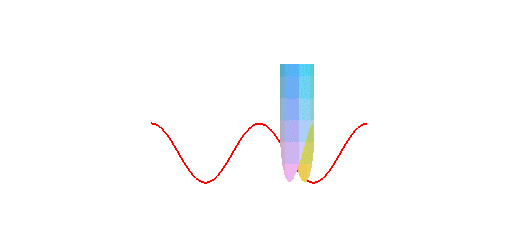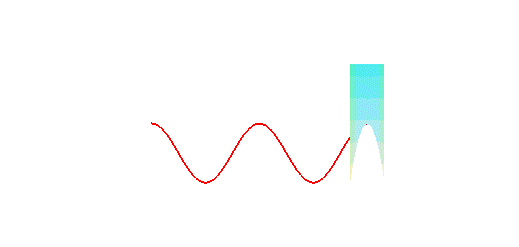
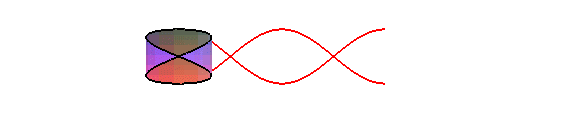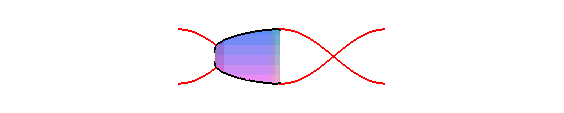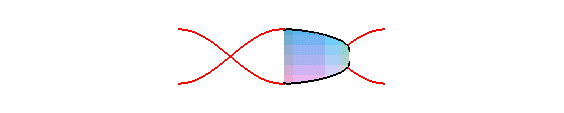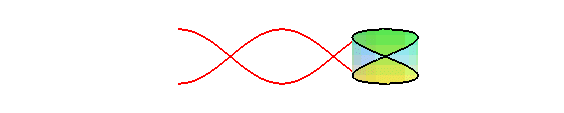
La projection orthogonale d'une hélice circulaire sur un plan parallèle à son axe est une sinusoïde.

Voir aussi la boite à œufs, la révolution de la sinusoïde, la surface du sinus.

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2022