Courbe étudiée par Chasles en 1875.

 

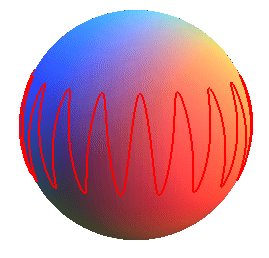
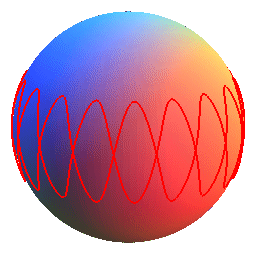
Équation sphérique :  . Paramétrisation cartésienne :   n > 0. Courbe algébrique pour n rationnel.

Les sinusoïdes sphériques sont les courbes sphériques qui se projettent par projection centrale du centre de la sphère sur un cylindre circonscrit à la sphère en une couronne sinusoïdale (laquelle se développe en une sinusoïde). Avec les données ci-dessus, cette sinusoïde a pour équation , où . Ce sont donc aussi les intersection d'un demi cône sinusoïdal avec une sphère centrée en son sommet.

Les projections centrales de centre O sur les plans perpendiculaires à Oz d'équation y = b, sont les épis : 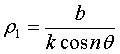, où .

Pour n  naturel, on obtient une courbe ayant n arches.
Pour n = 1 on obtient un grand cercle de la sphère (intersection de la sphère avec le plan z = kx) ; la paramétrisation ci-dessus fournit dont une paramétrisation des grands cercles de la sphère, excepté les méridiens.
 

Pour n = 2,  on obtient une courbe qui pourrait être la couture de la balle de tennis, intersection de la sphère  avec le demi-cône sinusoïdal : .

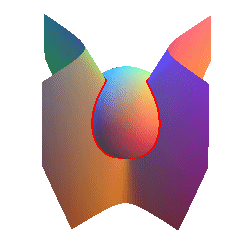Comparer avec les courbes des satellites.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2016