Curve studied by Chasles in 1875.

 

Spherical equation: . Cartesian parametrization:   n > 0. Algebraic curve when n is rational.

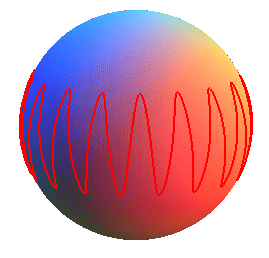
The spherical sinusoids are the spherical curves for which the central projection of the center of the sphere on a cylinder circumscribed to the sphere is a cylindrical sine wave (which in turn develops onto a sinusoid). With the parameters given above, the equation of this sinusoid is , where . Therefore, they also are the intersections between a half sinusoidal cone and a sphere centered on its vertex.

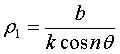
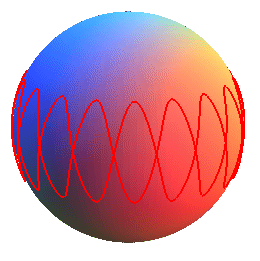
The central projections with center O on the planes perpendicular to Oz, with equation y = b, are the epispirals: , where .

When n is an integer, we get a curve with n arches.
For n = 1, we get a great circle of the sphere (intersection between the sphere and the plane z = kx); the above parametrization provides a parametrization of the great circles of the sphere, except the meridians.
 

For n = 2, we get a curve that could be the seam line of a tennis ball, intersection between the sphere with the half-sinusoidal cone: .

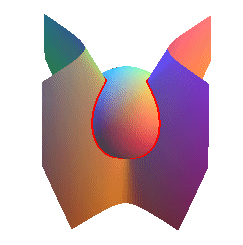Compare to the satellite curves.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018