SATELLITE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SATELLITE CURVE

| Homemade name.
See this paper named "Flowers and satellites". |
| Cartesian parametrization: that comes from In spherical coordinates
:
|
The satellite curves are the various trajectories of a
point M on a given great circle of a sphere rotating around one
of its axes, while M has a uniform motion along the circle.
These curves can also be seen as the trajectories of
points on a circle in uniform rotation around an axis, this axis being
itself in uniform rotation around an axis passing by the center of the
circle.
The name of satellite curve comes from the fact that the trajectory, in the frame associated to the Earth, of a satellite in uniform circular rotation around the center of the Earth is such a curve: see for example this book (pages 177 to 181).
In the above parametrization, the sphere centered on O
turns around Oz and the plane of the circle forms an angle
with respect to xOy; k is the ratio of the speed of rotation
of M on the circle over the speed of rotation of the sphere around
its axis.
Special cases of satellite curves include:
- the clelias
when the great circle meets the axis of rotation of the sphere ().
- the spherical
helices when
(in the second definition above, the circle rolls without slipping on a
fixed circle); it is the case where the curve has cuspidal points.
Examples:
 |
 |
 |
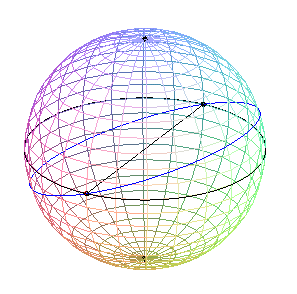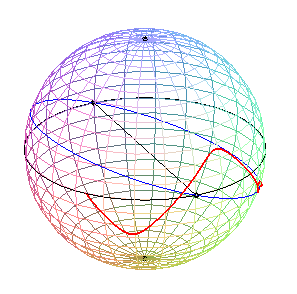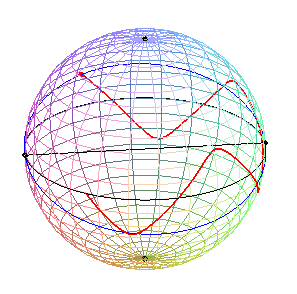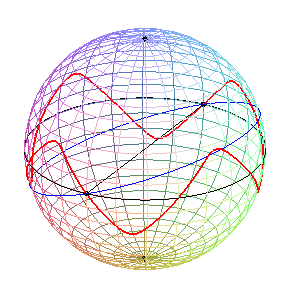
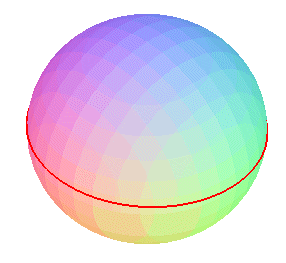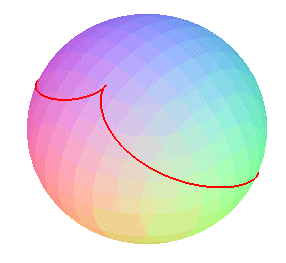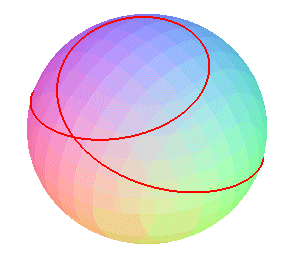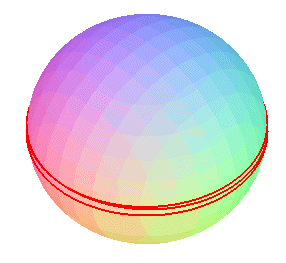
| k = 1 (rotation of the satellite equal to that
of the sphere)
The curve is none other than the hippopede of Eudoxus, that corresponds to geostationary trajectories. |
k =1/2 (speed of rotation of the satellite equal
to half that of the sphere)
Note the cusp corresponding to the spherical helix and the one corresponding to the clelia (passage by the poles) |
k = 2 (speed of rotation of the satellite equal
to twice that of the sphere)
The curve is none other than that of the seam line of a tennis ball, at least as long as it does not have double points. Note that there is a clelia, but no spherical helix. |
The linearization of the expressions of x and y
above
show that the projections on xOy of the satellite curves are
- for k > 1: hypotrochoids
with parameter 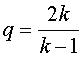
- for k < 1: epitrochoids
with parameter ,
which yields
.
See the Capareda
curves for a presentation of the satellite curves linked to this planar
projection.
Some examples for :
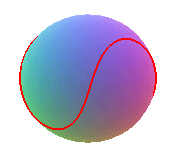
q = 4, k = 2 |
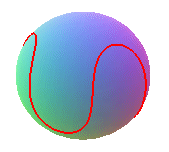
q = 6, k = 3/2 |
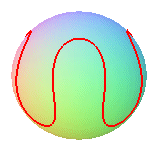
q = 8, k = 4/3 |

q = 3, k = 3 |
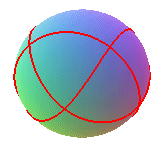
q = 8/3 , k = 4 |
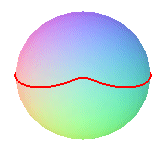
q = 4, k = 1/2 |
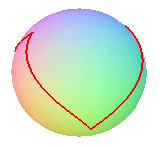
q = 6, k = 2/3 |
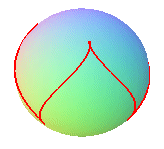
q = 8, k = 3/4 |

q = 3, k = 3 |

q = 8/3 , k = 4 |
Note that the satellite curves are not spherical
trochoids, except in the case of spherical helices, that also are spherical
cycloids.
However, the spherical trochoids and the satellite curves
can be reunited in the family of the curves that are the trajectories of
a point M of a fixed circle on a sphere in rotation around one of
its axes, M having a uniform motion on the circle.
The general Cartesian parametrization of these curves
is:
that comes from ;
a
is the distance to the axis, b the radius of the circle,
its inclination, k the ratio of speeds; the radius of the sphere,
centered on O, is
.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2018