
n = 1
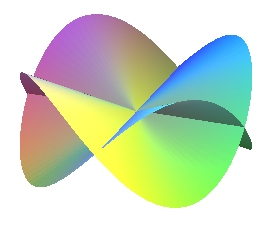
n = 2
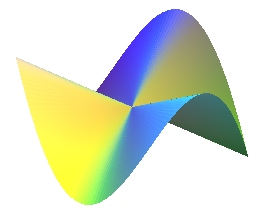
n = 3

n = 4
n =1/2
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
CÔNE SINUSOÏDAL
Sinusoidal
cone, Sinuskegel

n = 1 |

n = 2 |

n = 3 |

n = 4 |
|
n =1/2 |
|
| Équation cylindrique : Paramétrisation cartésienne : Surface algébrique pour n rationnel. |
La section par un cylindre d'axe Oz est la réunion de deux couronnes sinusoïdales (symétriques par rapport à O).
La section par une sphère centrée en O
est
la réunion de deux sinusoïdes
sphériques (symétriques par rapport à O).
La section par un plan horizontal z = b est un
épi
: 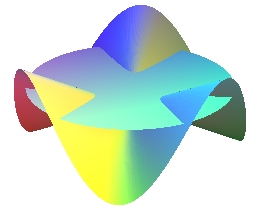 .
.
Comparer avec le conoïde
de Plücker.
| On peut aussi considérer le cône sécantoïdal,
d'équation cylindrique |
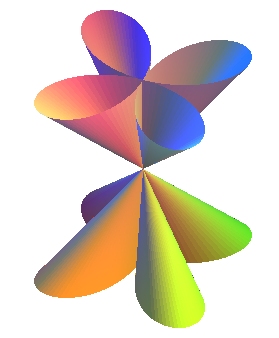 |
Epluchure de crayon, par Lévi Capareda
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2011