Dans son acception la plus générale, une surface à symétrie de rotation est une surface invariante par une rotation d'angle non nul.
Une surface est dite à symétrie de rotation d'ordre n si elle est invariante par une rotation d'un n-ième de tour (et non invariante par une rotation d'angle plus petit).
Une surface à symétrie de rotation d'ordre n peut ne pas avoir de plan de symétrie (voir par exemple les bouteilles de Klein d'ordre n), mais les surfaces à symétrie de rotation d'ordre n ayant un plan de symétrie passant par l'axe de rotation sont les surfaces ayant exactement n plans de symétrie passant par un même axe. Elles ont alors (au moins) les symétries d'une pyramide régulière à n faces latérales.

C'est la généralisation à l'espace de la notion de courbe à symétrie de rotation (et toutes les sections par des plans perpendiculaires à l'axe de rotation sont de telles courbes).
 
 

Équation cylindrique générale d'une surface à symétrie de rotation d'ordre multiple de n :	Équation cartésienne correspondante :
avec f  de plus petite période par rapport à  : ,	avec
Cas particulier :  (possède alors n plans de symétrie)	avec

Le cas  n = 2 est étudié à surface retournable (surface invariante par retournement).
Tout cylindre où cône droit de directrice une courbe à symétrie de rotation est une surface à symétrie de rotation.

Exemples de familles de surfaces algébriques à symétrie de rotation :
 

Nom	Équation polaire	Équation cartésienne	n = 2	n = 3	n = 4
Conoïde de Plücker		surface algébrique de degré n+1 pour n pair,  de degré 2n +2 pour n impair		rem : la symétrie est d'ordre 6
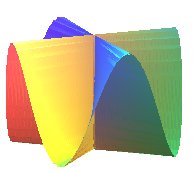
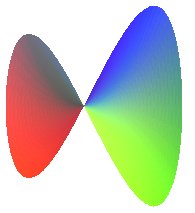
Selle pour pieuvre		surface algébrique de degré n	selle de cheval	selle pour singe
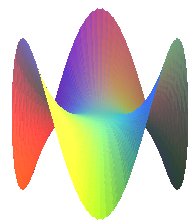
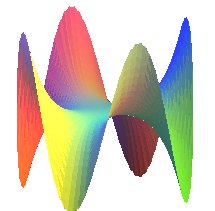
Cône sinusoïdal		surface algébrique de degré n pour n impair,  de degré 2n pour n pair	rem : symétrie d'ordre 4		rem : symétrie d'ordre 8
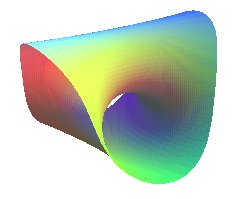
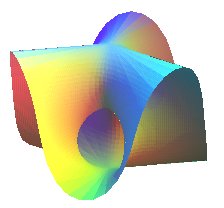
??		surface algébrique de degré n+1 pour n pair,  de degré 2n +2 pour n impair	cyclide parabolique
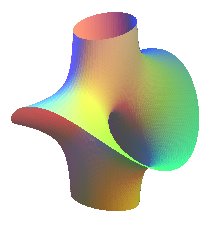
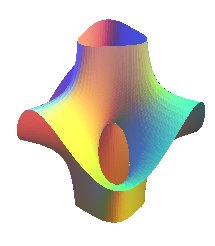
Surface de Costa algébrique		surface algébrique de degré n+1 pour n pair,  de degré 2n +2 pour n impair

 
 

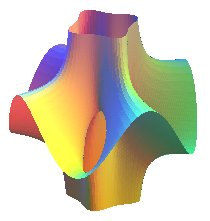En ce qui concerne les surfaces paramétrées, on obtient une large famille de surface à symétrie de rotation d'ordre n en prenant  où  f est une fonction complexe - périodique par rapport à sa première variable, et g, de même, mais réelle. Par exemple, pour , on obtient la surface ci-contre, dans laquelle apparait une structure en anti-diamant. La surface de Morin d'ordre n est aussi une telle surface.

Plusieurs familles de surfaces minimales sont à symétrie d'ordre n :

Les surfaces d'Enneper , les surfaces de Richmond, les n - noïdes, et les surfaces de Costa-Hoffman-Meeks.

Comme autres surfaces présentant des symétries, voir aussi les surfaces de Goursat.

Suirface à symétrie d'ordre 5, par Patrice Jeener, avec son aimable autorisation

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2014