SURFACE DE COSTA
Costa surface,
costasche Fläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE COSTA
Costa surface,
costasche Fläche
| Surface étudiée par da Costa en 1982.
Celso José da Costa (1949-....) : mathématicien brésilien. fr.wikipedia.org/wiki/Surface_de_Costa mathworld.wolfram.com/CostaMinimalSurface.html |
Paramétrisation de
Gray :  ,  ,
où 
désigne la fonction
dzeta de Weierstrass associée au couple (c,0) (WeierstrassZeta[z,
{c, 0}] en mathematica),
désigne la fonction
P
de Weierstrass également associée au couple (c,0)
(WeierstrassP[z,
{c, 0}] en mathematica)
c et 
sont deux constantes associées aux fonctions de Weierstrass égales
respectivement à 189,7272... et 6,87519.... |
Jusqu'en 1982 il était conjecturé que les seules surfaces minimales complètes (i.e. sans bord), sans auto-intersection et non périodiques étaient : le plan, le caténoïde et ses surfaces associées. La surface de Costa, et d'autres ensuite, sont venues infirmer cette conjecture.
On l'obtient en prenant 
dans la paramétrisation de Weierstrass d'une surface
minimale : 
.
|
La surface de Costa est invariante par retournement autour de l'axe x = y, z = 0 (dans la paramétrisation ci-dessus, y(u,v)=x(v,u) et z(v,u)=-z(u,v)), et dans ce retournement, les deux faces de la surface sont échangées. Ci-contre, deux demi-surfaces. Vérifier que l'une est le retournement de l'autre. |
  |
||
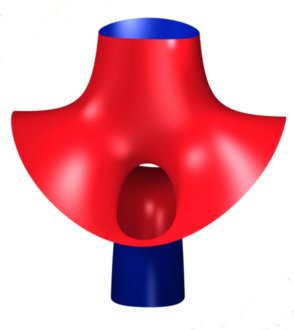
| Animation de la surface dont les deux faces sont coloriées
de deux couleurs.
Imaginer de l'eau versée à l'intérieur de l'entonnoir supérieur ; elle ressortira sur la face extérieure de l'entonnoir inférieur... |
|
La surface de Costa est topologiquement équivalente
à un tore moins 3 points (elle est donc de genre
1) .
Elle est aussi topologiquement très proche de
la surface algébrique cubique
d'équation cartésienne très simple :  ,
elle aussi invariante par un
retournement échangeant les deux faces.
Noter que les sections horizontales de cette dernière surface sont des ellipses ou des hyperboles. Noter aussi que cette surface est asymptote pour x
et y grands au conoïde de
Plücker
|
 |
La surface de Costa se généralise à une surface à symétrie de rotation d'ordre n.
Comparer la surface de Costa avec la surface
minimale de Riemann finie, qui possède également une
nappe plane et deux nappes évasées, mais qui s'intersecte
elle-même.
Surface de Costa, par Alain Esculier |
Surface de Costa par Patrice Jeener, avec son aimable autorisation |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2014
