SURFACE MINIMALE DE RIEMANN FINIE
Finite
Riemann minimal surface, endliche riemannsche Minimalfläche
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE MINIMALE DE RIEMANN FINIE
Finite
Riemann minimal surface, endliche riemannsche Minimalfläche
| Surface étudiée par David Hoffman et Hermann
Karcher en 1993.
Liens : virtualmathmuseum.org/Surface/lopez-ros/lopez-ros.html minimal.sitehost.iu.edu/research/claynotes.pdf p 29 |
Paramétrisation cartésienne : 
avec  .
Les vues de cette pages sont faites avec k = 3/10. |
La surface minimale de Riemann finie est la surface
minimale obtenue en prenant 
(puis 
)
dans la paramétrisation de Weierstrass d'une surface
minimale : 
.
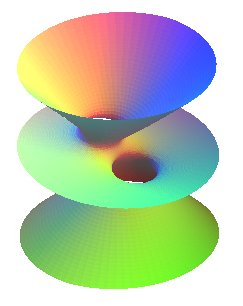
Elle possède 2 nappes infinies du type de celles
du caténoïde et une
nappe infinie asymptote à un plan (d'où l'appellation "finie",
par opposition à la surface
minimale de Riemann originelle ayant une infinité de nappes
planaires).
Notons que si on les prolonge, les nappes s'intersectent,
contrairement à celles de la surface
de Costa.
La surface minimale de Riemann finie a même forme
que les surfaces cubiques d'équations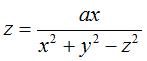 
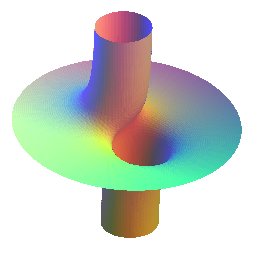
et  .... |
cylindre asymptote x²+y²=a² |
|
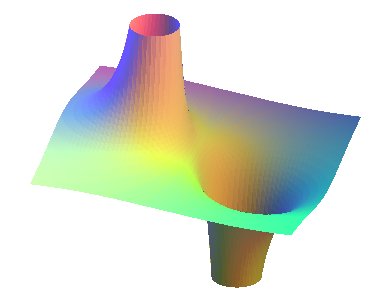
... ou encore que la surface sextique d'équation  ,
ainsi que la surface transcendante d'équation  .
Les deux ont pour droites asymptotes les droites  . |
 |
 |
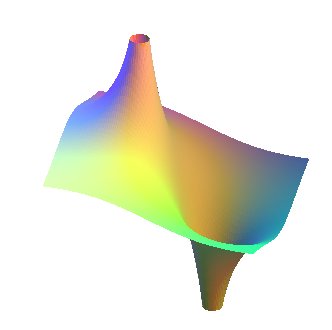Une Riemann finie, par Alain Esculier. |
Une Riemann finie en fil de fer par Christoph Soland, Gymnase du Bugnon, Lausanne, voir à surface de Dyck. |
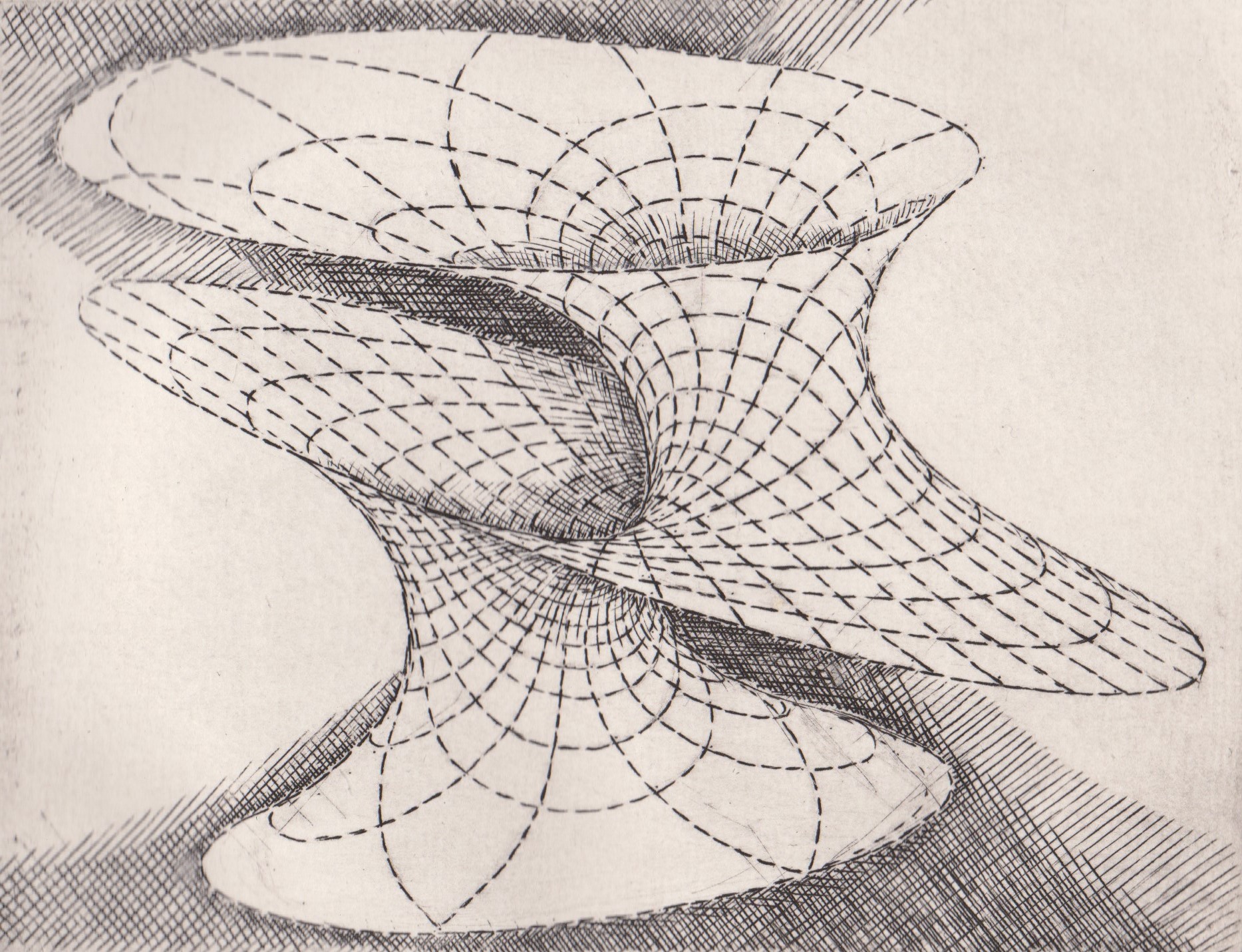
Gravure de cette surface, par Patrice Jeener
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2015