SURFACE DE DYCK
Dyck's surface,
Dycksche Fläche

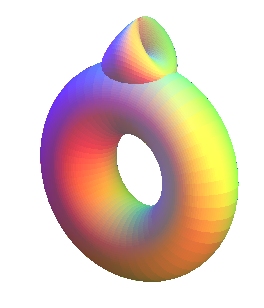
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE DYCK
Dyck's surface,
Dycksche Fläche

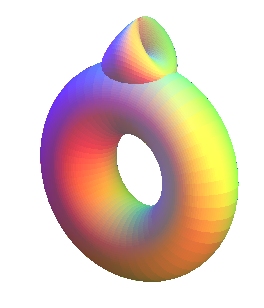
| Surface étudiée par Von Dyck en 1888.
Walther Von Dyck (1856-1934) : mathématicien allemand. |
En 1888, Walther von Dick montrait que la somme
connexe de 3 plans projectifs
était topologiquement équivalente à la somme connexe
d'un tore avec un plan projectif
(). Cette surface
à deux formes est appelée depuis surface de Dyck.
Concrètement, si l'on part d'une surface homéomorphe
à la sphère (nous avons pris ci-dessus un cube), on obtient
en découpant 3 disques dans cette surface et en cousant bord à
bord 3 rubans de Möbius (nous
avons pris ci-dessus des bonnets croisés troués), et on obtient
en découpant un disque dans un tore, et en cousant bord à
bord un ruban de Möbius.
Notons que si
et
sont
équivalents,
et
ne
le sont pas (
est la bouteille de Klein).
La surface de Dyck est caractérisée par
le fait que c'est une surface compacte connexe sans bord
- unilatère de genre
2,
ou - de caractéristique
d'Euler-Poincaré -1.
| Christoph Soland a une vision plus esthétique
de la surface de Dyck que les représentations ci-dessus.
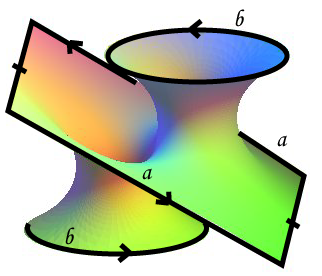
Il part de la surface minimale de Riemann finie ci-contre qu'il imagine dans l'espace projectif de dimension 3. Les deux bords b des nappes en caténoïde sont alors identifiés comme indiqué et le bord a,a, de la nappe centrale subit une identification similaire à celle du plan projectif. Par aplatissement, on obtient l'ovale à deux trous ci-contre, et par chirurgie, l'octogone situé en dessous. Les 8 arêtes étant identifiées 2 à 2, et les huit sommets 4 à 4, cet octogone a 1 face, 4 arêtes et 2 sommets, S-A+F=-1 : c'est la surface de Dyck. |
 |
|
| Christoph Soland a réalisé cette surface en sculpture de fil de fer qu'il a baptisée "janus bifrons" (dieu à 2 têtes). Elle est exposée au gymnase du Bugnon, Lausanne, Suisse. |
 |
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERREOL 2014