DYCK'S SURFACE

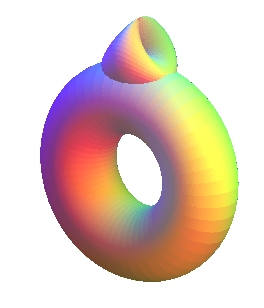
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DYCK'S SURFACE

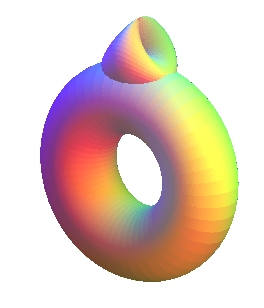
| Surface studied by Von Dyck in 1888.
Walther Von Dyck (1856-1934): German mathematician. |
In 1888, Walther von Dick proved that the connected sum of 3 projective planes is topologically equivalent to the connected sum of a torus and a projective plane
(). This surface with two shapes has been called ever since Dyck's surface.
In concrete terms, if we begin with a surface homeomorphic to the sphere (above, we took a cube), we get by cutting 3 disks in this surface and sew edge to edge 3 Möbius strips (above, we took punctured cross-caps), and we get
by cutting a disk inside a torus, and sewing edge to edge a Möbius strip.
Note that much as and
are equivalent,
and
are not (
is the Klein bottle).
Dyck's surface is characterized by the fact that it is a compact connected surface without boundaries
- with one side and of genus 2,
or - with Euler characteristic equal to -1.
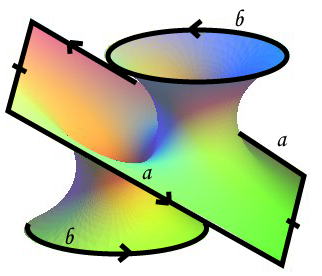
| Christoph Soland has a more aesthetic vision of Dyck's surface than the above representations.
He starts from the finite Riemann minimal surface opposite which he imagines in the projective space of dimension 3. The two edge b of the catenoid-like sheets are identified as indicated and the edge a,a, of the central sheet undergoes an identification similar to that of the projective plane. By flattening, we get the oval with two holes opposite, and by surgery, the octagon just below. The 8 edges being identified 2 by 2, and the eight vertices 4 by 4, this octagon has 1 face, 4 edges and 2 vertices, S-A+F=-1: it is Dyck's surface. |
 |
|
| Christoph Soland made this wire sculpture of the surface and called it "janus bifrons" (god with two heads). It is displayed in the Bugnon gymnasium, Lausanne, Switzerland. |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017