DINI'S SURFACE
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
DINI'S SURFACE
| Surface studied by Dini in 1865.
Ulisse Dini (1845-1918): Italian mathematician. Other names: Dini's helicoid, pseudospherical helicoid. |
| Cartesian parametrization: First fundamental quadratic form: Gaussian curvature: |
| Dini's surface is the surface generated by the application
of a screw to a tractrix
along its asymptote, in other words, the helicoid
with generatrix a tractrix and axis the asymptote of this tractrix.
Its most important property is to have constant total curvature, like the pseudosphere (which is generated by the rotation of a tractrix around its asymptote). Another of its properties is to be the only helicoid the curvature lines of which are meridians (Bianchi theorem, cf. [gray] p. 483). Opposite, rotation of a half of Dini's surface around its axis. |
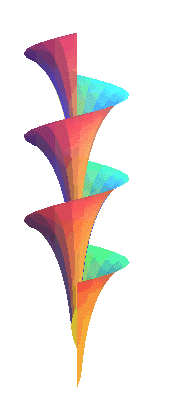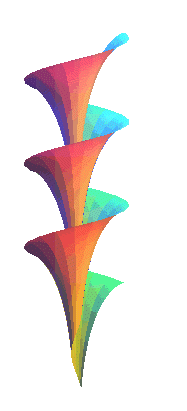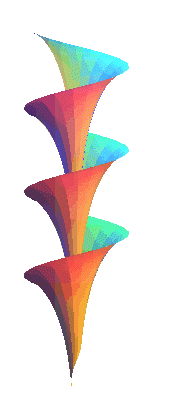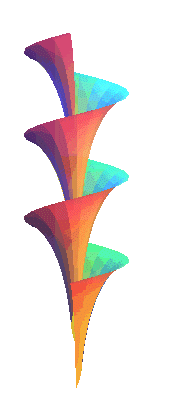 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017