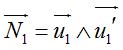,
and the generatrix of the first sheet is directed by 
,
we obtain the director vector 
of the second sheet by calculating 
, 
, 
,
where 
is the reflection with respect to the plane orthogonal to 
;
we have then 
.| next surface | previous surface | 2D curve | 3D curves | surfaces | fractals | polyhedra |
FOLDED DEVELOPABLE SURFACE
| Notion studied by Fuchs and Tabachnikov in 1999 [More
on paper folding, The American Mathematical Monthly, 106, p. 27-35],
and by Pottmann and Walner in 2001 [Computational Line Geometry, Springer, 2001, p 416-422] See also: Folding Curves, by Robert Geretschläger. |
When two developable surfaces contain the same curve, and that curve has the same geodesic curvature in every point in respect to the two surfaces, the planes tangent to the two surfaces form the same angle with the plane osculating at the curve, in all points thereof and are therefore either equal or symmetrical with respect to this plane.
Recall that the geodesic curvature is the curvature of
the curve obtained by developing the surface. So if we fold a sheet of
paperboard along a space curve, we obtain on both sides
of the curve two developable surfaces having the forme property. If the
first surface is known, the second is uniquely defined by the fact that
it is the envelope of symmetric planes of the planes tangent to the first
with respect to the osculating planes along the curve.
| If the curve of the fold is generated by the point ,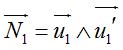
and the generatrix of the first sheet is directed by ,
we obtain the director vector
of the second sheet by calculating , , ,
where
is the reflection with respect to the plane orthogonal to ;
we have then . |
| Example: if the fold is flat, the folded portion is the sheet symmetrical with respect to the plane thereof. Opposite, case of a cone and of a parabolic cylinder. |  |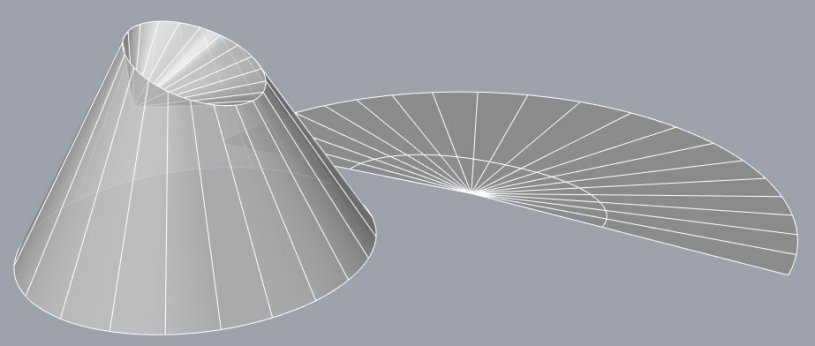
 |
Formulas in the case of a fold in a cylinder
of revolution:
Cylinder  ,
folding curve :  .
The generatrix of the folded part have as director vector :  .
|
| Concrete experience with strong paper.
On the right, gooseneck bagger. |
 |
 |
 |
|
Mathematical modeling of the winding of the cylinder. The generatrix of the folded part here have a constant length, and do not model the rectangular paper sheet. Note that at the midpoint, the fold is flat, and therefore the folded part is the symmetrical half-cylinder. Parametrization of the cylindrical part : |
 |
Pictures from Robert March. |
| Link to great achievements in folded virtual paper. |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019
, 
: the folded part is the culinder of revolution symetrical with respect
to the fold's plane.
, 
.
, 
.
.
,
and 
, u
between
0 and 1, et the animation from 
.