Equation of the cylinder with radius R and axis (O, ) with : . Cylindrical equation: . Cartesian equation:  . Cartesian parametrizations:  or  (cf figure on the right). Developable quadric. First fundamental quadratic form:  . Surface element:  . Second fundamental quadratic form: .

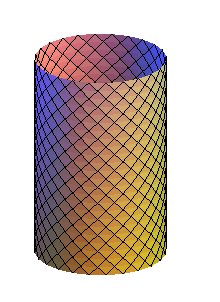Parametrization the coordinate lines of which form a double lattice of orthogonal circular helices, which are also the rhumb lines at 45° of this cylinder (be it placed horizontally or vertically).

The cylinder of revolution is the surface generated by the revolution of a line parallel to an axis, around this axis.
The cylinder can be developed by mapping a point M to the point of the plane with Cartesian coordinates  .
Remarkable curves traced on the cylinder of revolution:
 - curvature lines: the circles z = constant and the generatrices.
 - geodesics, helices and rhumb lines: the circles z = constant, the generatrices, and the circular helices.

See also the cylindrical curves, and the equidomoids.

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017