Cartesian equation of a cylinder with axis orthogonal to (a, b, c) and (a', b', c') : . For a cylinder with axis Oz : Cartesian equation: . Cartesian parametrization: 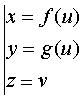. First fundamental quadratic form: . Second fundamental quadratic form: .

The cylinders (or cylindrical surfaces) are the ruled surfaces the generatrices of which have a fixed direction .
A curve traced on the cylinder which meets all the generatrices is called a directrix of the cylinder; there exists a unique cylinder with given direction and directrix.

Necessary and sufficient condition: surface globally invariant under the action of any translation in the direction .
We can also consider that a cylinder is a cone the vertex of which is at infinity.
Cylinders are translation surfaces, developable surfaces and moulding surfaces.

The lines of curvature are the generatrices and their normal sections.

The word cylinder is also used in a topological sense and refers to any surface homeomorphic to the cylinder of revolution, or, which amounts to the same thing, to a sphere minus two points. For example, an open strip with an even number of half-turns is topologically equivalent to a cylinder.

See also the cylindrical catenaries.

 
 
 
 
 

next surface

previous surface

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2020