ELLIPTICAL CYLINDER

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ELLIPTICAL CYLINDER

Cartesian equation: 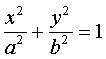 (of revolution
if and only if a = b).
(of revolution
if and only if a = b).
Developable quadric. |
The elliptical cylinders are the cylinders
with an ellipse as directrix.
| Contrary to appearances, every elliptical cylinder contains
circles, intersections between the cylinder and the planes forming an angle It can therefore be constructed by hanging strings between two circles, the strings being parallel to the line joining the two centers. |

Two circular sections of an elliptical cylinder |
| The arches of the cupola of the Duomo in Florence are
arcs of circles. The cupola is therefore composed of 8 portions of elliptical
cylinders. See this
page for more explanations.
See also the echo room at Chaise-Dieu, on this page. |
 |
See also the spherical ellipses, and the focal cubics.

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017