Courbe étudiée par Bobillier en 1829.

 

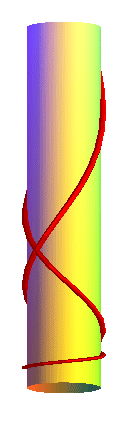	Équation différentielle :  (voir à chaînette générale), où  est le vecteur normal au cylindre. Cas du cylindre vertical : Équation différentielle en coordonnées cylindriques (avec ): ,  d'où la Paramétrisation cylindrique : .
Cas z0 = 0	Cas du cylindre horizontal d'axe Ox : Équation différentielle en coordonnées cylindriques  définies par ( avec ) : . Intégrale première : . Paramétrisation cylindrique dans le cas  : (intégrale elliptique de première espèce).

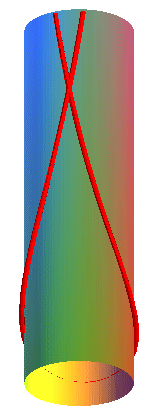
La chaînette cylindrique est la ligne d'équilibre d'un fil pesant infiniment mince, homogène, flexible et inextensible inclus dans un cylindre de révolution, en présence d'un champ de pesanteur uniforme.
 
 

Lorsque le cylindre est vertical, les chaînettes cylindriques sont les courbes qui se développent en des chainettes planes d'axe vertical (et c'est le cas pour tout cylindre vertical général).

 

Lorsque le cylindre est horizontal, on obtient une courbe en forme de sinusoïde courbée oscillant autour du faîte ou de  la ligne de base, ou bien une courbe en hélice autour du cylindre. Le seul cas de courbe fermée est celui des cercles verticaux. Pour le faîte, l'équilibre n'est stable que si l'on prend une portion inférieure à une période. Ci-contre, seule la courbe verte est en équilibre stable ; la courbe rouge va tomber d'un côté ou de l'autre.

 

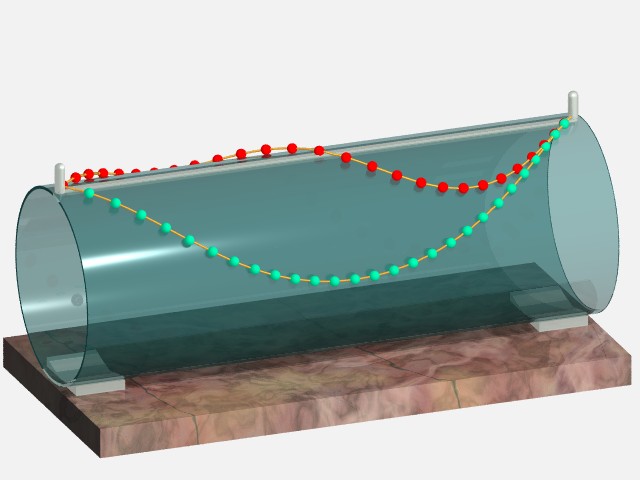Une expérience réelle :	Un exemple dans le cas oblique :

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL, Alain ESCULIER 2004