Cylindrical catenary

CYLINDRICAL CATENARY

Curve studied by Bobillier in 1829.

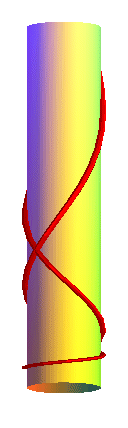Differential equation: (see at general catenary), where is the normal vector of the cylinder.
Case of the vertical cylinder:
Differential equation in cylindrical coordinates (with ): , hence the
Cylindrical parametrization: .

Case z₀ = 0

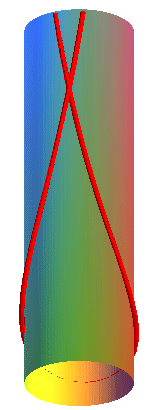
Case of the horizontal cylinder with axis Ox:
Differential equation in cylindrical coordinates defined by (with ):
.
First integral:
.
Cylindrical parametrization in the case :
(elliptic integral of the first kind).

The cylindrical catenary is the equilibrium line of an inelastic flexible homogeneous infinitely thin massive wire included in a cylinder of revolution, placed in a uniform gravitational field.

When the cylinder is vertical, the cylindrical catenaries are the curves that develop into planar catenaries with vertical axis (and it is so for any general vertical cylinder).

When the cylinder is horizontal, we get a curve shaped like a curved sinusoid oscillating around the top or the base line, or a curve shaped like a helix around the cylinder. The only case of closed curve is that of vertical circles.
For the curve oscillating around the top, the corresponding equilibrium is only stable if we consider a portion smaller than a period.
Opposite, only the green curve is in a stable equilibrium; the red curve will fall on one side or the other.

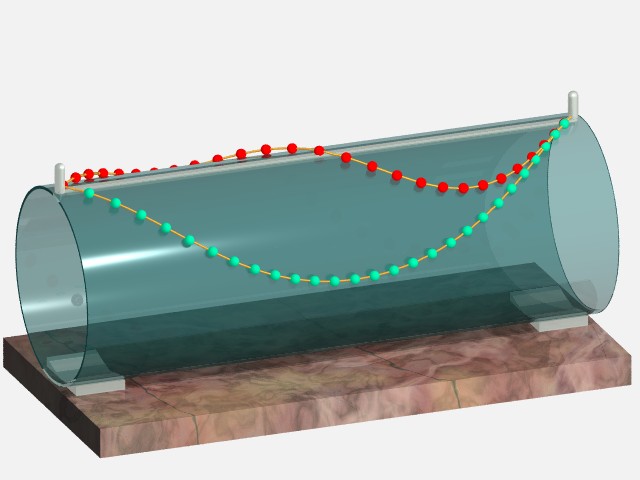A real experiment: An example in the slanted case:

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

	Differential equation: (see at general catenary), where is the normal vector of the cylinder. Case of the vertical cylinder: Differential equation in cylindrical coordinates (with ): , hence the Cylindrical parametrization: .
Case z₀ = 0	Case of the horizontal cylinder with axis Ox: Differential equation in cylindrical coordinates defined by (with ): . First integral: . Cylindrical parametrization in the case : (elliptic integral of the first kind).