CONICAL CATENARY
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONICAL CATENARY
| Curve studied by Bobillier in 1829. |
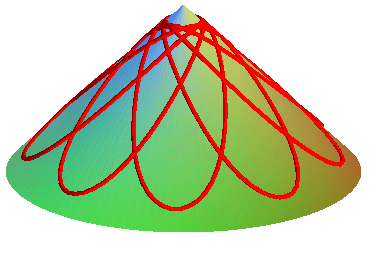
The conical catenary is the equilibrium line of an inelastic flexible homogeneous infinitely thin massive wire included in a cone of revolution, placed in a uniform gravitational field.
Differential equation: 
(see at general catenary),
where 
is the normal vector of the cone.
Case of the vertical cone with vertex O and half-angle a, parametrization based on the polar coordinates |
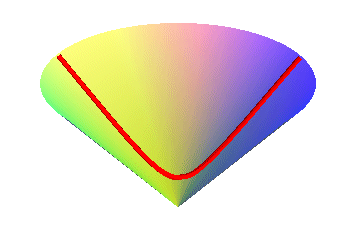
(but that is not a hyperbola!) |
Differential equation in the case where  : 
Parametrization: 
(rectangular hyperbola in the development plane). |
|
|
   |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL,
Alain ESCULIER 2018
of the development plane: 
.
(with 
).
Notice that it does not depend on a.