Notion studied by Bobillier in 1829. See: Paul Appell: cours de mecanique rationnelle, page 220.

 

Differential equation: , where  is the normal vector of the surface.

The catenaries of a surface are the equilibrium lines of an inelastic flexible homogeneous infinitely thin massive wire included in the surface, placed in a uniform gravitational field.

The catenaries are also the curves that minimize the altitude of their center of gravity, which means that the catenary with length l that joins A and B is, among all the homogeneous curves with length l joining A and B traced on the surface, the one with center of gravity at the lowest altitude.

Here is the derivation of the above differential equation:
 

We write the force equilibrium relation for a small element of the wire: ( = tension of the wire at M,  = weight,  = normal reaction of the surface), which gives: (1)  (m = linear mass density of the wire,  = vector tangent to the curve). But applying the Binet formulas, we get:  where  is the normal vector of the surface. Multiplying  by  yields , i.e. , hence ; by substituting this value for T in (1), we derive the differential equation.

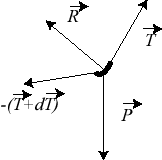Examples:

    - the catenaries of a non horizontal plane are the usual catenaries.

    - the catenaries of any vertical cylinder are the curves that develop into catenaries with vertical axis.

    - the cylindrical catenaries

    - the conical catenaries

    - the spherical catenaries
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2018