Notion studied by Catalan in 1843 (J. E. P.,1843, 29e cahier, pages 121-156), Delaunay in 1843 ( J. M.,1843, vol. 8, pages 231-244), Darboux in 1883 (C. R.,1883, vol.96, p.54) , and Whittemore in 1901. See also  [Blaschke p. 99]

 

Differential equation for a surface , with the classic notations: .

The notion of geodesic circle is the generalization to any surface of the notion of circle in the plane.

There are two major definitions, that are not equivalent in general:

DEF 1: locus of the points of the surface located at given geodesic distance (the geodesic radius) from a center (located on the surface).

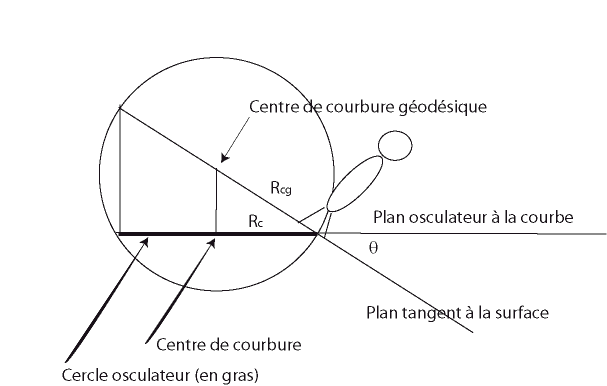
DEF 2: maximal curve with constant nonzero geodesic curvature - the case of zero curvature gives the geodesic lines. The radius of this geodesic circle is then the reciprocal of its curvature. In other words, the sphere that contains the osculating circle of the curve and the center of which is in the tangent plane of the surface has a constant radius. Figuratively, this definition corresponds to the trajectories of observers moving on a surface turning left or right with a constant angle, or of small cars the direction of which is blocked in a given position. Nota: geodesic circles are not, in general, skew circles (with constant curvature).

Whittemore proved that these two notions coincide for surfaces with constant Gaussian curvature, which are the surfaces that are applicable to a plane (in other words, developable), a sphere, or a pseudosphere.
Delaunay proved that, just as in the plane, the closed curves with minimal length enclosing a given area, or with given length enclosing the larger area, are the geodesic circles in the second sense (isoperimetric property).
According to Gauss' lemma, the geodesic circles (definition 1) with given center are the orthogonal trajectories, on the surface, of the geodesics passing by this center [Pressley p. 245].

Examples:
     - the geodesic circles of the plane or the sphere are the usual circles (but, be careful: circles (in the classic sense) traced on a surface are not, in general, geodesic circles)

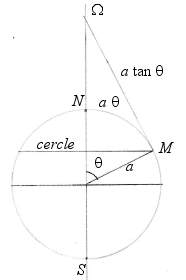
Parallel circle with colatitude  on the sphere with radius a: with the first definition, it has two centers N and S, and two radii  and ; with the second definition, its radius is . Note that its length is . The equator has radius  with the first definition, and  with the second one (it is a geodesic).

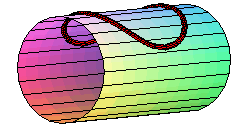
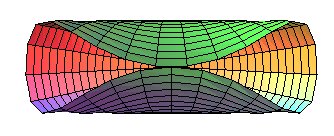
     - the geodesic circles of a cylinder or a cone, and more generally of developable surfaces, are the curves that give circles when the surface is applied onto a plane; concretely, geodesic circles can be seen as the edges of circular pancakes applied onto the surface.

Special case of the cylinder of revolution:

Parametrization for a geodesic circle with radius b on a cylinder with radius a: . It has double points as soon as its diameter is greater than or equal to the cylinder's circumference (). Compare to the pancake curve .		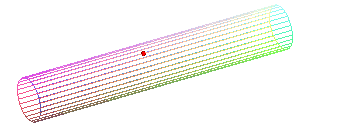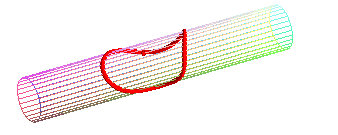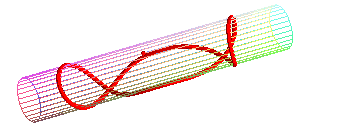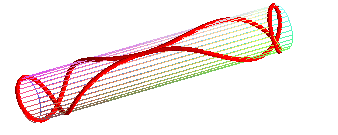When its radius is equal to the circumference of the cylinder, the "circle" passes by its center...
Parametrization of the cylinder by the polar geodesic coordinates, the coordinate lines of which are circular helices and geodesic circles: .

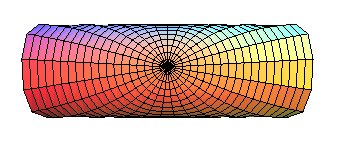Special case of the cone of revolution:

Parametrization for a geodesic circle with radius b, center located a distance a from the vertex of a cone with half-angle :  Remark: for fixed u and variable b, the above formula gives the geodesics passing by the center of the circle. See the special case a = b on the page of the cone of revolution.

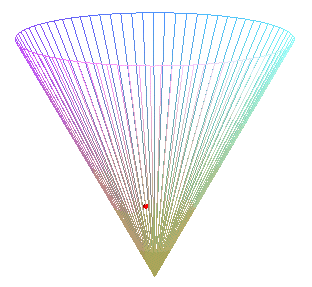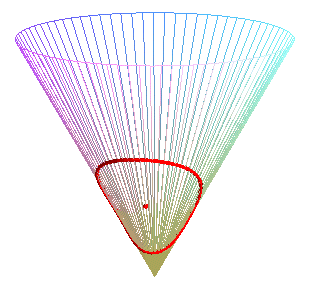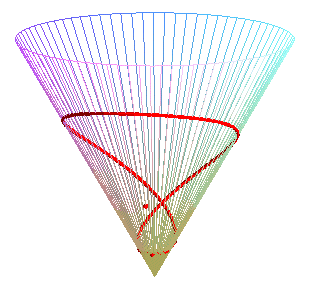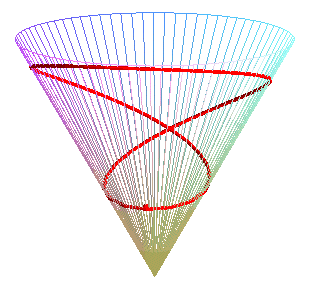
Animation for a circle with radius ranging from 0 to 2a.

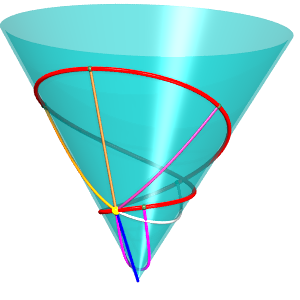
At the end of this animation, the circle passes by its center. Some geodesics passing by the center (yellow point) are traced.

 
 

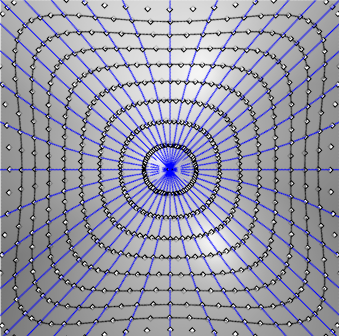
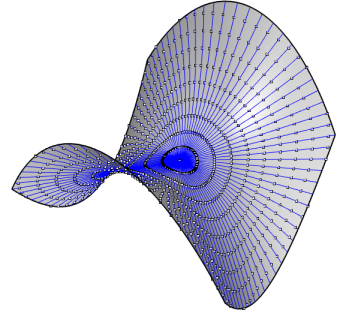
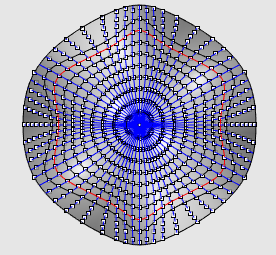
A case where the two definitions are not equivalent: the rectangular hyperbolic paraboloid. On this figure are traced the geodesics passing by O and the points at given geodesic distance from O, that show the geodesic circles of the first definition. Through some calculation, it can be noticed that the geodesic curvature is not constant along these circles. Figures made thanks to Rhinoceros by Robert March.
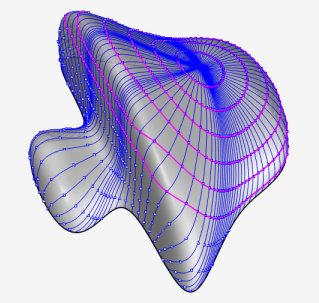
Other example: the monkey saddle.
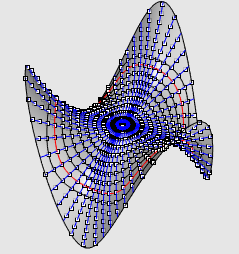Third example: the torus (see also the specific page on geodesics).

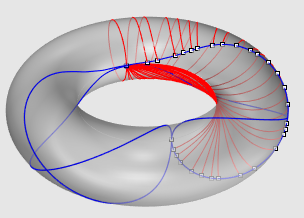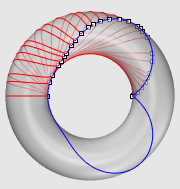The geodesic ellipses have also been defined as the loci of the points for which the sum of the geodesic distances from two fixed points is constant.
For example, the curvature lines of the ellipsoid are the geodesic ellipses with foci the umbilics.

next curve

previous curve

2D curves

3DÂ curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2018