SELLE POUR SINGE
Monkey
saddle, Affensattel

| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SELLE POUR SINGE
Monkey
saddle, Affensattel


| Équation cylindrique : Paramétrisation cartésienne : Équation cartésienne : Surface cubique. |
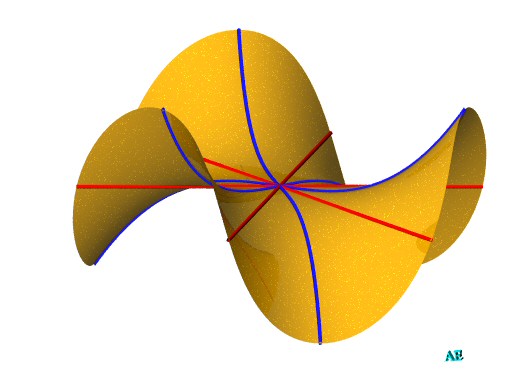
Surface en forme de selle permettant de mettre les pattes mais aussi la queue du singe (le singe n'étant pas ici la monture, mais le cavalier !).
Par le point O (qui est un méplat
de la surface) passent 3 droites réelles de la surface, faisant
entre elles des angles de 120° (en rouge ci-dessus) : le point O
est un point d'Eckardt de la surface
; par le point à l'infini de Oz, qui est point singulier
de la surface, passent les 3 autres droites de la surface, qui sont également
réelles, mais à l'infini.
O est aussi un ombilic.
| Généralisation : surface à col où
aboutissent n vallées et n montagnes : Le cas n = 2 donne la selle de cheval ou paraboloïde hyperbolique et le cas n = 3 la selle pour singe. Proposition d'appellation par Paul Micaelli : selle pour pieuvre... |
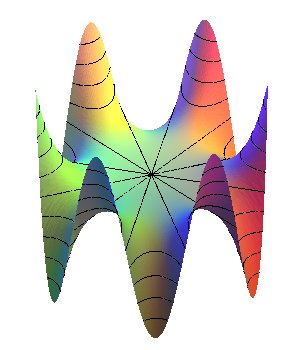 |
| Autre surface avec 3 vallées, 3 montagnes : |
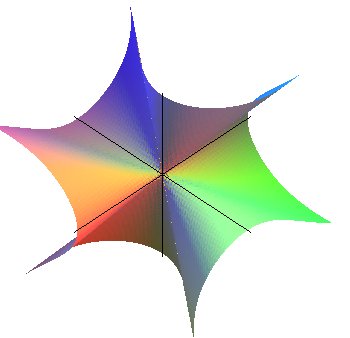 |
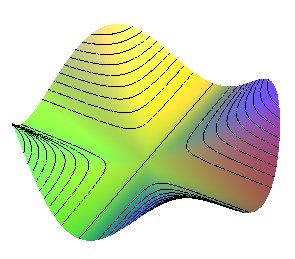
| Surface avec 4 montagnes, 4 vallées, plates cette
fois : |
 |
Comparer avec la surface
d'Enneper.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2020