Surfaces étudiées par Seifert en 1934. Herbert Seifert (1907-1996) : mathématicien allemand. Sites : Wikipedia anglais Logiciel seifertview à télécharger

Une surface de Seifert associée à une courbe fermée lisse sans auto-intersection de l'espace (autrement dit, un représentant d'un noeud) est une surface compacte connexe orientable sans auto-intersection ayant pour bord cette courbe.
Le théorème de Seifert assure l'existence de cette surface, non unique, bien sûr.
 
 

Si le disque est évidemment une surface de Seifert associée au noeud trivial, on pourrait penser obtenir une surface de Seifert associée au noeud de trèfle, en joignant par un segment chaque point de la courbe au point le plus éloigné de lui sur la courbe. Cependant, la surface obtenue n'est autre que le ruban de Moebius à 3 demi-tours, qui n'est pas orientable.

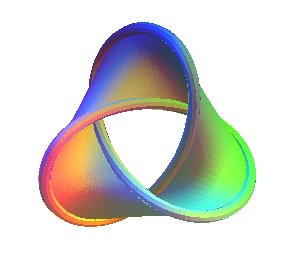
Pour obtenir une surface de Seifert de bord le noeud de trèfle, on peut faire circuler un segment partant d'un couple de sommets hauts vers un couple de sommets bas, ceci trois fois (figure du centre), et compléter les deux triangles. La surface obtenue a bien deux faces (noter par exemple que la face supérieure du triangle supérieur conduit à la face supérieure du triangle inférieur).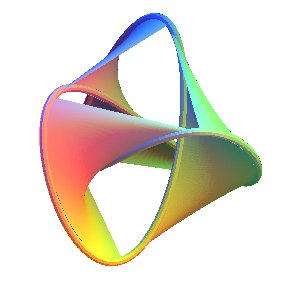
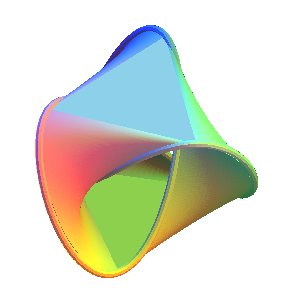En stylisant, voilà ce que cela pourrait donner (à gauche, une vue perso, à droite, une vue obtenue par le logiciel seifertview)

 

La notion de surface de Seifert s'étend aux entrelacs. Ci-contre, l'exemple de l'entrelac de Hopf ; la surface a été obtenue par circulation d'un segment joignant les deux disques (comme pour les exemples antéprécédents, c'est donc une portion de surface réglée).

Le noeud de trèfle et l'entrelacs de Hopf font partie des entrelacs toriques de type (p, 2 ) auxquels on peut appliquer le même procédé que ci-dessus pour obtenir une surface de Seifert ; ci dessous les 4 premiers exemples :
 

type de l'entrelac	(2,2) : entrelac de Hopf	(3,2) : noeud de trèfle	(4,2) : noeud de Salomon entrelac premier 412	(5,2)
Représentation en table aux pieds tordus réalisée par Alain Esculier
Représentation arrondie (obtenue par seifertview)

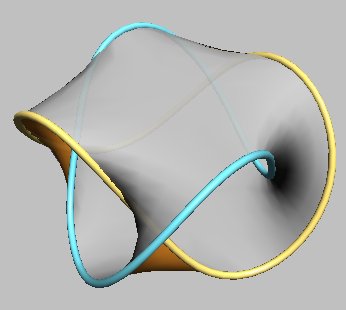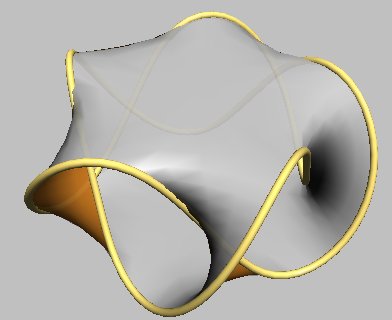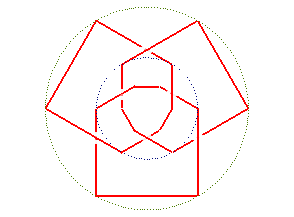
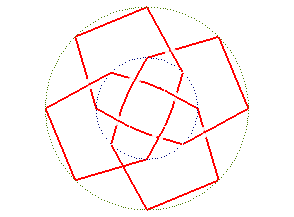
On peut "rajouter un plateau" à la table ci-dessus ; en tordant les montants supérieurs en sens contraire des inférieurs, on obtient 3 noeuds ou entrelacs remarquables :

	double table à 2 pieds :  noeud de huit	double table à 3 pieds :  anneaux de Borromée	double table à 4 pieds : noeud premier 818
Représentation en table aux pieds tordus réalisée par Alain Esculier
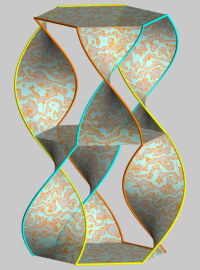Noeud en projection conique
Représentation arrondie (seifertview)

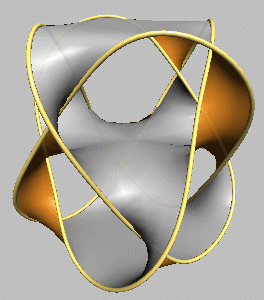Plus généralement, une table à p plateaux et q montants, avec des montants tordus tous dans le même sens, correspond à l'entrelac torique de type (p, q).
Tout noeud et entrelac peut être représenté par cette méthode, avec un nombre quelconque de plateaux et de montants, eux-même ayant un nombre quelconque de torsions.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2022