Surfaces étudiées par Schwarz en 1864, puis par A. H. Schoen en 1970, qui a donné les abréviations "P" et "D". Hermann Amandus Schwarz (1843-1921) : mathématicien allemand. Sites : wikipedia anglais Vues povray de cette page réalisées par Alain Esculier

 

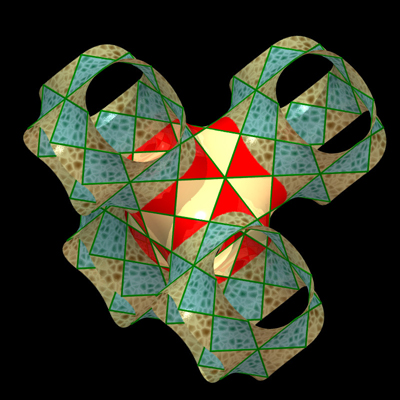
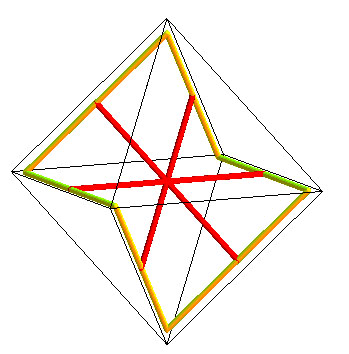
La surface minimale "D" (comme diamant) de Schwarz est la surface minimale triplement périodique ayant pour motif de base la solution du problème de Plateau pour un contour qui est l'un des 6 quadrilatères gauches construit à partir d'un hexagone gauche inscrit dans les arêtes d'un cube comme représenté ci-contre. La surface minimale "P" (comme primitive) de Schwarz est la surface construite de manière similaire à la précédente à partir d'un hexagone gauche inscrit cette fois dans les arêtes d'un octaèdre régulier.

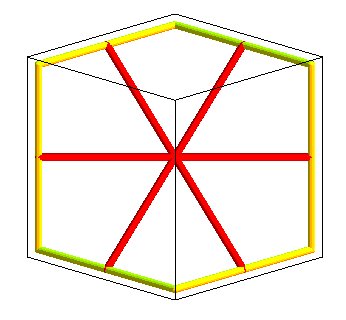Hexagone gauche, base de la surface D de Schwarz, formé de 6 quadrilatères gauches ; les arêtes jaunes sont 6 des 12 arêtes d'un cube. Chaque quadrilatère de Plateau a 3 angles droits et un de 60° et deux côtés égaux à rac(2) fois les 2 autres.

Hexagone gauche, base de la surface P de Schwarz, formé de 6 quadrilatères gauches ; les arêtes jaunes sont 6 des 12 arêtes d'un octaèdre régulier. Chaque quadrilatère de Plateau a 2 angles droits et 2 angles de 60°, et 4 côtés égaux.

La solution de Plateau pour un quadrilatère gauche n'est pas, comme on pourrait le penser hâtivement, une portion de paraboloïde hyperbolique (PH) dont les génératrices sont ses côtés, et on trouvera, ici pour Schwarz D, et ici pour Schwarz P, le calcul exact de cette solution (et on verra dans ces articles que les deux surfaces sont conjuguées par la transformation de Bonnet) : la paramétrisation de Weierstrass est obtenue avec ,  pour D et  pour P. Dans les vues ci-contre des 6 surfaces s'appuyant sur les 6 quadrilatères gauches, on a utilisé une méthode de triangulation donnant aussi une surface s'appuyant sur le contour considéré, mais qui n'est pas la surface de Plateau ; la méthode est détaillée en bas de cette page.

Hexagone de base de Schwarz D

Hexagone de base de Schwarz P

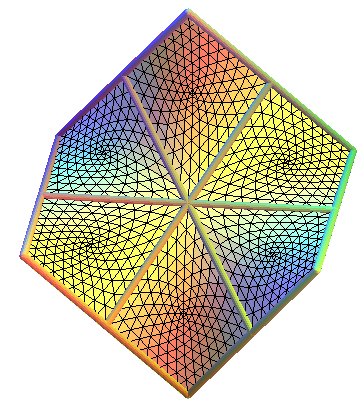
La surface D de Schwarz complète est obtenue en effectuant les 6 symétries par rapport aux 6 côtés de l'hexagone de base et en réitérant à l'infini.		La surface complète est obtenue par translations de ce composé de 4 hexagones de base.
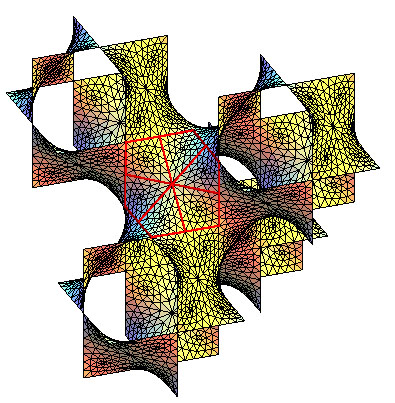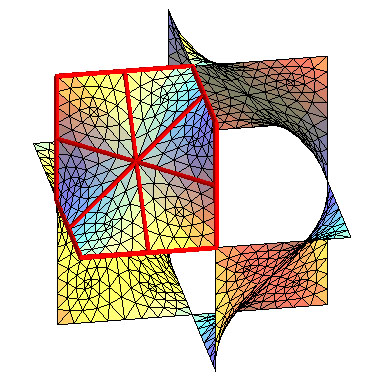Idem pour la surface P.		La surface complète est obtenue par translations de ce composé de 12 quadrilatères de base. Il est à noter que cette surface est minimale mais n'est pas la surface d'aire minimale s'appuyant sur les carrés supérieurs et inférieurs...

 

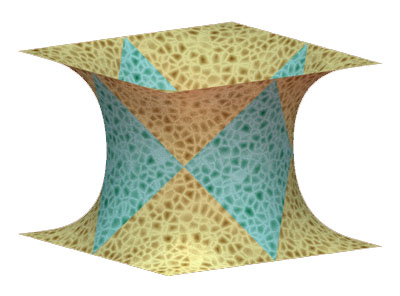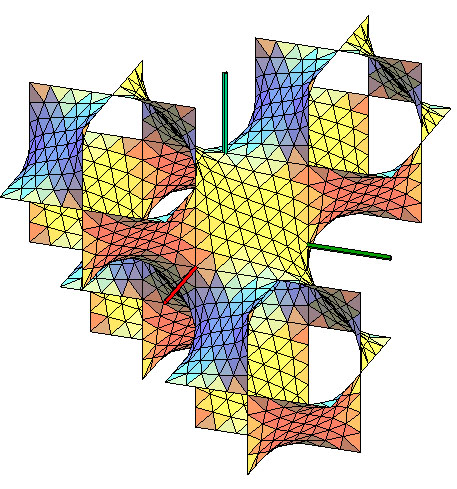
La surface P complète peut être vue comme un réseau de tuyaux se croisant à angle droit (d'où le surnom de "plumber's nightmare" = "cauchemard du plombier")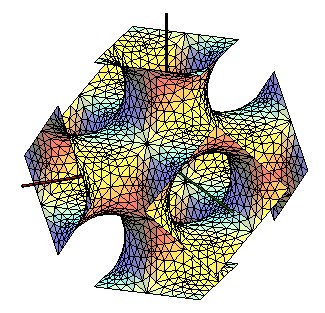

Motif composé de 36 quadrilatères élémentaires.  En remplaçant les quadrilatères de Plateau par des portions de paraboloïdes hyperboliques, on obtient la sculpture d'Angel Duarte à Lausanne.

Si l'on rogne la moitié de 24 quadrilatères du motif précédent on obtient un motif engendrant la surface entière par translations.

Cette construction de béton montre comment la surface complète est construite à partir du motif précédent, et montre aussi que la surface partage l'espace en deux parties connexes superposables (l'intérieur des tuyaux est isométrique à l'extérieur).

 

La surface D complète peut être vue comme un réseau de tuyaux se croisant à angles de 109°28', comme les segments joignant le centre d'un tétraèdre régulier aux 4 sommets. Là aussi, l'intérieur des tuyaux est superposable à l'extérieur.
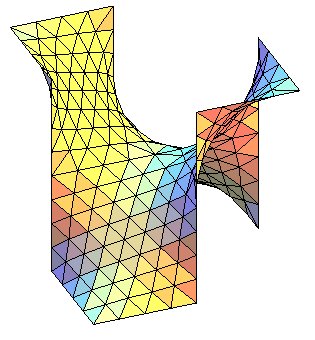
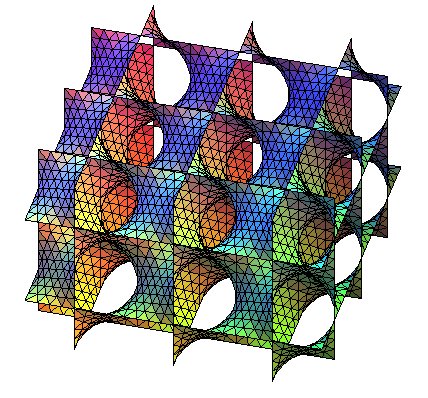
Une autre façon de construire la surface D finale est de construire d'abord cette selle formée de 4 hexagones de base, puis de la dupliquer par translations :

 

Les surfaces D et P sont approchées par les surfaces dites "nodales" d'équations cartésiennes respectives : et , elles aussi triplement périodiques, mais non minimales.

Surface D approchée res:=90:maxi:=5*Pi/2:f:=(x,y,z)->if x+y+z<maxi and x-y-z<maxi  and -x+y-z<maxi and -x-y+z <maxi then cos(x)*cos(y)*cos(z) -sin(x)*sin(y)*sin(z) else NULL fi:   implicitplot3d(  'f'(x,y,z), x=-maxi..maxi ,y=-maxi..maxi, z=-maxi..maxi,grid=[res,res,res],style=patchnogrid,lightmodel=light2,scaling=constrained,orientation=[140,25]);

Surface P approchée

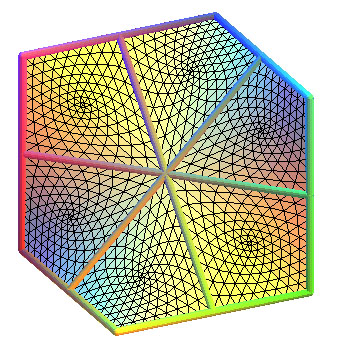
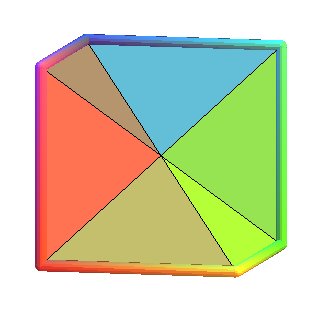
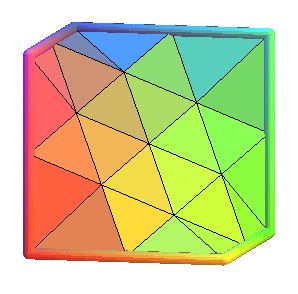
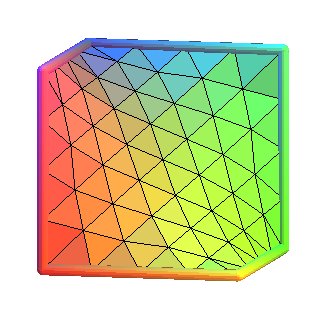
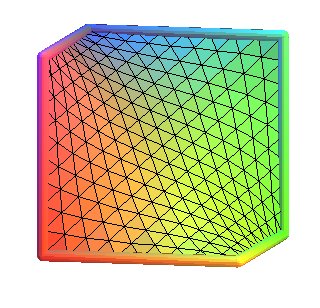
Explication du procédé de triangulation ci-dessus, non sur un quadrilatère, mais sur l'hexagone gauche de la surface D directement :
On part des 6 triangles délimités par les 3 diagonales du contour ; puis pour chaque triangle, on introduit 3 points "correspondant" un peu à chaque milieu des côtés, avec 2 cas :
Si le côté est sur le contour : le point est réellement le milieu du coté.
Si le côté n'est pas sur le contour : le point est le le barycentre des sommets des deux faces ayant ce coté en commun (donc les extrémités du coté commun comptent deux fois ).
Le triangle est alors partagé en 4 petits triangles dont les sommets sont ceux du triangles de départ plus les 3 points introduits.
Voici les 5 premières étapes de ce procédé, avec la cinquième étape tracée sans les triangles :

Voir aussi la surface de Néovius et le gyroïde, surfaces minimales ayant la même représentation de Weierstrass que les surfaces D et P, mais un autre angle de Bonnet.

Schwarz D

Schwarz P

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  Alain ESCULIER 2011