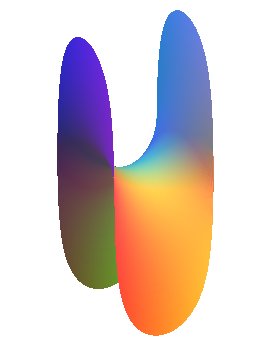
surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

SURFACES DE SCHERK
Scherk surfaces, Scherksche Flächen


Surfaces étudiées par Scherk en 1834.
Heinrich Ferdinand Scherk (1798-1885) : mathématicien allemand.
Les hélicoïdes minimaux sont aussi parfois appelés surfaces de Scherk.

Première surface de Scherk

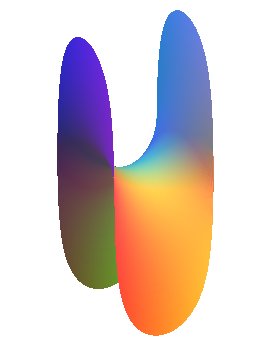
Équation cartésienne : , soit , .
Forme équivalente : .
Droites incluses : , et .
Paramétrisation de Weierstrass :  avec  et , ce qui donne : 
Surface minimale de translation doublement périodique.

La première surface de Scherk est la seule surface minimale qui soit de translation. Elle est obtenue par translation de la courbe du log cosinus (qui est aussi la chaînette d'égale résistance) le long d'elle même.

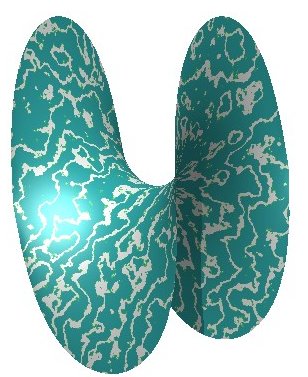
Modèle de la surface de Scherk réalisé par Jean-Marie Dendoncker et son élève Julie, modèle montrant bien la définition comme surface de translation.
 
Voir ici une surface de Scherk en légo !

 
 

Vue réalisée avec Povray par Alain Esculier
Surface de Scherk approchée réalisée en film de savon ;
photo de Jean-Marie Dendoncker.

Comparer avec la surface d'Enneper, autre surface minimale.

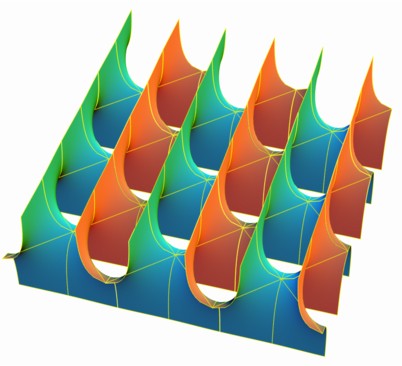
Deuxième surface de Scherk

Équation cartésienne : . 
Surface minimale simplement périodique.

Gravure de la première surface de Scherk, par Patrice Jeener, avec son aimable autorisation.


surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

© Robert FERRÉOL  2011