SURFACE DE TRANSLATION
Translation
surface, Schiebefläche (oder Translationsfläche)
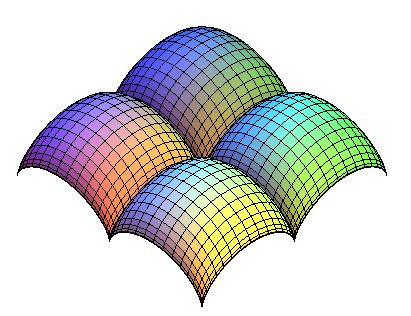
Translation d'une cycloïde le long d'une cycloïde.
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
SURFACE DE TRANSLATION
Translation
surface, Schiebefläche (oder Translationsfläche)

Translation d'une cycloïde le long d'une cycloïde.
| Paramétrisation cartésienne : Lorsque les génératrices sont planes : Équation cartésienne (cas particulier) : Équation aux dérivées partielles : |
Une surface de translation est une surface qui
est réunion de courbes translatées les unes des autres ;
c’est donc une surface résultant de la translation
d’une courbe (première génératrice) le long d’une
autre (deuxième génératrice) ; cette définition
est symétrique en ce sens que la translation de la deuxième
génératrice le long de la première donne la même
surface.
 |
Par exemple, la surface |
Une surface de translation est donc un cas particulier
de surface de Darboux.
La somme de Minkovski de deux sous-ensembles
et
de
l'espace étant définie comme l'ensemble des points M
tels que
où
décrit
et
décrit
,
une surface de translation peut donc être définie comme la
somme de Minkovski de deux courbes.
On obtient une définition équivalente en considérant les surfaces lieux géométriques des milieux des segments dont les extrémités décrivent deux courbes ("midsurface" en anglais, "Sehnenmittenfläche" en allemand).
Exemples :
- le plan (cas où les deux
génératrices sont des droites)
- les cylindres
(cas où la première génératrice est une droite)
- les paraboloïdes
hyperbolique et elliptique
(les deux génératrices sont des paraboles), seules quadriques
de translation.
- l'hélicoïde
droit (les deux génératrices sont des hélices
circulaires)
- le dôme
de Bohème (les deux génératrices sont des cercles)
- la boite
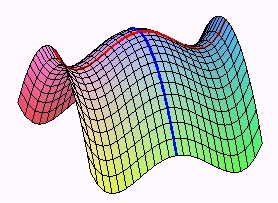
à œufs (les deux génératrices sont des sinusoïdes)
- la révolution
de la sinusoïde (les deux génératrices sont des
hélices circulaires)
- la surface
de Scherk
| Translation d'une portion de chaînette le long
d'une portion identique : Ceci modélise-t-il la suspension d'un filet à mailles perpendiculaires, voire d'un drap ? |
 |
et les surfaces z = f(x) g(y) ?
| surface suivante | surface précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2025