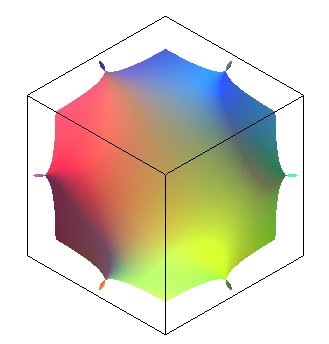
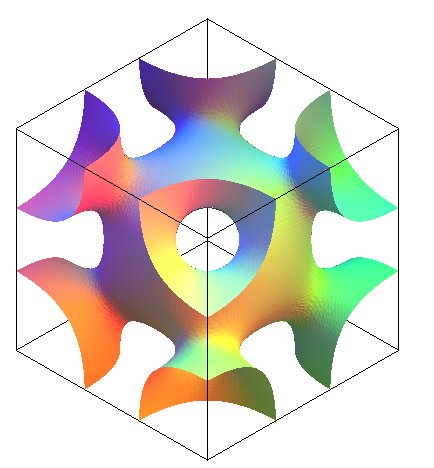
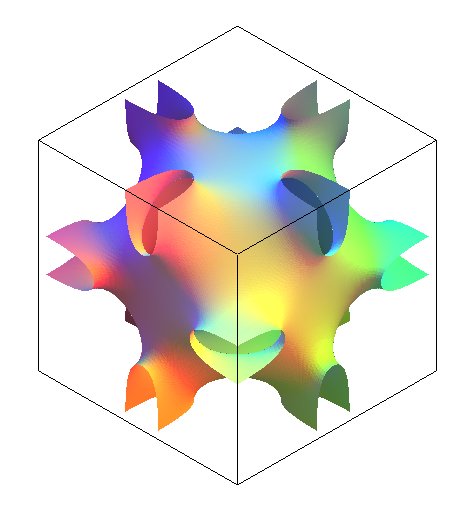
La surface de Néovius est une surface
minimale triplement périodique dont le pavé élémentaire,
reproduit ci-contre, possède 12 ouvertures centrées sur les
arêtes d'un cube, donc aux sommets d'un cuboctaèdre
(comparer avec le pavé élémentaire 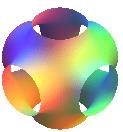 de
la surface P de Schwarz,
qui possède 6 ouvertures centrées sur les faces d'un
cube). de
la surface P de Schwarz,
qui possède 6 ouvertures centrées sur les faces d'un
cube).
La figure ci-contre a été réalisée
à partir de l'équation 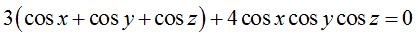 qui donne une surface, dite "nodale", non minimale, proche de la véritable
surface de Néovius.
qui donne une surface, dite "nodale", non minimale, proche de la véritable
surface de Néovius.
|
 |
La surface de Néovius complète sépare
l'espace en deux composantes connexes, isométriques entre elles,
comme pour la surface P de Schwarz (une translation de vecteur 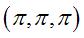 laisse globalement invariante la surface, mais échange les faces).
laisse globalement invariante la surface, mais échange les faces).
Au dessus, au centre, imaginer une cellule identique à
ses voisines venant s'encastrer dans le creux. |
 |
qui donne une surface, dite "nodale", non minimale, proche de la véritable
surface de Néovius.