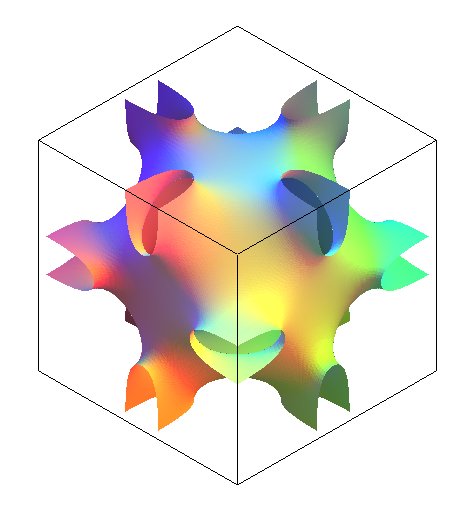
The figure opposite was made thanks to the equation
which gives a surface, said to be "nodal", that is non minimal, close to
the true Neovius surface.
Above, at the center, imagine an cell identical to its neighbors, embedded in the hollow.

| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
NEOVIUS SURFACE
| Surface studied by Neovius
in 1883.
Edvard Rudolf Neovius (1851-1917): Finish mathematician. Websites: Wikipedia |
| The Neovius surface is a triply periodic minimal
surface the fundamental patch of which, reproduced opposite, has 12
openings centered on the edges of the cube, hence at the vertices of a
cuboctahedron
(compare to the fundamental patch The figure opposite was made thanks to the equation |
 |
| The fundamental patch is composed of eight skew dodecagons of the type opposite: |
 |
| The complete Neovius surface splits the space into to
connected components, isometric to one another, like the Schwarz P
surface (a translation with vector Above, at the center, imagine an cell identical to its neighbors, embedded in the hollow. |
 |
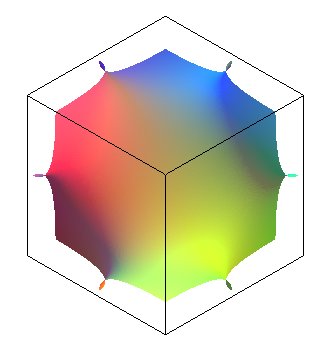
| View of an elementary cell (intersected by a sphere instead of a cube) with its 12 openings. | View of its connections of 6 of its 12 neighbors. | View of the cubes containing each cell.
Production: Alain Esculier. |
 |
 |
 |
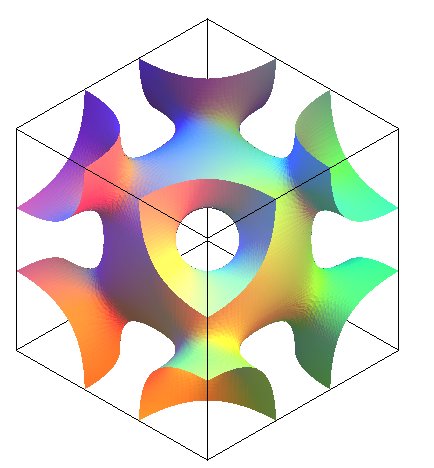
| Another minimal surface, discovered by Alan Schoen, has
a fundamental patch with 8 opening located at the vertices of the cube
(abbreviation I-WP)
Its approximate nodal equation is The complete surface is composed of cubes connected by
their vertices.
|
 |
 |
Also compare to the gyroid.
|
Patch of the Neovius surface, by Patrice Jeener, with his kind authorization. |

Anaglyph 3D image of the Neovius surface, by Alain Esculier,
|
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017