SURFACE RÉGLÉE
Ruled
surface, Regelfläche
Une surface réglée est une surface
qui est réunion de droites, appelées ses génératrices.
On lui associe son cône directeur, réunion des droites
passant par un point donné et parallèles aux génératrices.
Par trois courbes passe en général une unique
surface réglée, réunion des droites rencontrant ces
trois courbes. Si les trois courbes sont algébriques de degrés
respectifs p,q,r, la surface est "en général" algébrique
de degré
2pqr.
| La famille des droites s'appuyant sur deux courbes données
n'engendre en général pas une surface ; mais c'est le cas
si l'on rajoute une condition supplémentaire, comme : |
Les exemples ci-dessous montrent diverses surfaces réglées
s'appuyant sur un demi-cercle et une demi-ellipse : |
| 1) les droites doivent rencontrer une troisième
courbe donnée (donc famille des droites s'appuyant sur 3 courbes) |
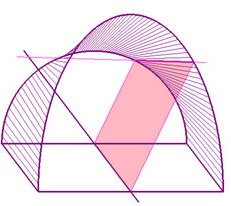
la troisième courbe est une droite
|
| 2) elles doivent être parallèle à
un plan "directeur" donné (surface
de Catalan) |
|
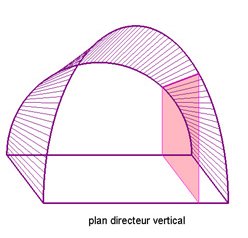
| 3) la surface est développable
(donc enveloppe de la famille des plans tangents communs aux deux courbes,
plans obtenus en prenant une tangente à une courbe, et une tangente
à l'autre, sécante à la première) |
|
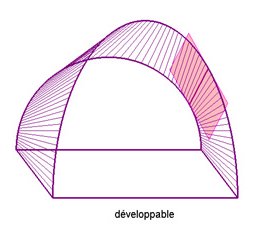
| 4) la distance entre les deux points de contact est constante
(voir les exemples du berlingot
et de l'oloïde) |
|
Les points d'une surface réglée sont hyperboliques
ou paraboliques ; lorsqu'un point est parabolique, tous les points
de sa génératrice le sont et ont le même plan tangent
: la génératrice est dite parabolique ; ceci arrive lorsqu'elle
est tangente à la ligne
de striction et correspond au cas où le paramètre de
distribution est nul.
Exemples :
- les cônes,
les cylindres, et plus généralement
les surfaces développables
(cas où toutes les génératrices sont paraboliques).
- les conoïdes
(dont le paraboloïde
hyperbolique) et plus généralement les surfaces
de Catalan (cône directeur plan)
- les surfaces
conoïdales (dont le berlingot)
et plus généralement les surfaces
réglées à directrice rectiligne.
- les hyperboloïdes
à une nappe.
- les hélicoïdes
réglés (dont l’hélicoïde droit et l’hélicoïde
développable).
- la surface
de Möbius et plus généralement les surfaces
réglées de Cayley.
- la surface d'Hector
Guimard.
- des exemples de surfaces
de Seifert.
Les quadriques
propres réglées sont les surfaces réunions des droites
rencontrant trois droites deux à deux non coplanaires : paraboloïde
hyperbolique dans le cas où les trois droites sont parallèles
à un plan fixe et hyperboloïde
à une nappe dans l'autre cas ; ce sont les seules surfaces doublement
réglées (i.e. qui sont réunion de deux familles
de droites distinctes).
Les surfaces cubiques
réglées sont les cônes et cylindres de directrice
une cubique, les surfaces conoïdales du 3ème degré et
les surfaces réglées de Cayley.
Les surfaces de révolution réglées
sont les hyperboloïdes
à une nappe.
Voir aussi leurs cousines les surfaces
cerclées.
Palissades à La Villette, Paris (2014) |
Caténaires midi formant d'élégantes
surfaces réglées |
© Robert FERRÉOL
2011, Robert March 2003
.
,
réunion des génératrices Du
passant par 
et dirigées par 
(en simplifié : 
)
; cône directeur : 
.
.
, senestre si 
; elle est développable
ssi d = 0.
où 
est la distance entre Du
et Du+du
et 
,
l'angle entre Du
et Du+du
.