Indicatrice de Dupin

INDICATRICE DE DUPIN
Dupin's indicatrix, Dupinsche Indikatrix

Notion introduite par Dupin en 1813.
Charles Dupin (1784-1873) : économiste, mathématicien et homme politique français.

Lorsqu’un plan parallèle au plan tangent en un point M d’une surface tend vers celui-ci, sa section avec la surface tend à devenir homothétique d’une courbe qui, normalisée convenablement, est l’indicatrice de Dupin du point de cette surface.
Lorsque le point n’est pas un méplat, l’indicatrice de Dupin est la réunion de deux coniques, d'équation dans le plan tangent rapporté aux directions principales, où R₁ et R₂ sont les rayons de courbure principaux de la surface en M. Ces directions principales sont données par les deux lignes de courbure passant par le point.

Lorsque R₁ et R₂ sont finis de mêmes signes, l’indicatrice est une ellipse, et le point est dit elliptique (et appelé ombilic quand R₁ = R₂).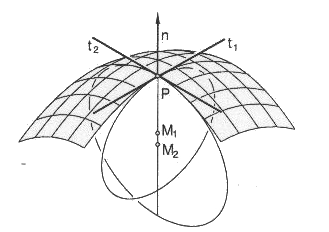

Lorsque R₁ et R₂ sont finis de signes contraires, l’indicatrice est la réunion de deux hyperboles conjuguées, et le point est dit hyperbolique ; les deux asymptotes de ces hyperboles sont les tangentes asymptotiques en M, tangentes aux deux lignes asymptotiques passant par M.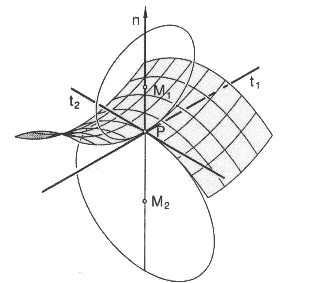

Lorsque R₁ ou R₂ est infini, l’indicatrice est la réunion de deux droites parallèles, et le point est dit parabolique ou torsal.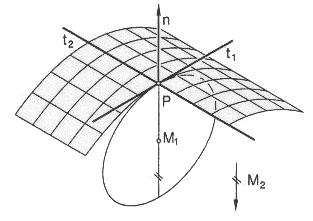

surface suivante surface précédente courbes 2D courbes 3D surfaces fractals polyèdres

Lorsque R₁ et R₂ sont finis de mêmes signes, l’indicatrice est une ellipse, et le point est dit elliptique (et appelé ombilic quand R₁ = R₂).
Lorsque R₁ et R₂ sont finis de signes contraires, l’indicatrice est la réunion de deux hyperboles conjuguées, et le point est dit hyperbolique ; les deux asymptotes de ces hyperboles sont les tangentes asymptotiques en M, tangentes aux deux lignes asymptotiques passant par M.
Lorsque R₁ ou R₂ est infini, l’indicatrice est la réunion de deux droites parallèles, et le point est dit parabolique ou torsal.